题目内容
10.计算$\sqrt{12}×\sqrt{\frac{1}{3}}+\sqrt{5}×\sqrt{3}$的结果在( )| A. | 4至5之间 | B. | 5至6之间 | C. | 6至7之间 | D. | 7至8之间 |
分析 先计算$\sqrt{12}×\sqrt{\frac{1}{3}}+\sqrt{5}×\sqrt{3}$的结果,然后估算结果的大小,即可解答本题.
解答 解:$\sqrt{12}×\sqrt{\frac{1}{3}}+\sqrt{5}×\sqrt{3}$
=$2\sqrt{3}×\sqrt{\frac{1}{3}}+\sqrt{15}$
=2$+\sqrt{15}$,
∵$\sqrt{9}<\sqrt{15}<\sqrt{16}$,
∴$3<\sqrt{15}<4$,
∴$5<2+\sqrt{15}<6$,
故选B.
点评 本题考查二次根式的混合运算、估算无理数的大小,解题的关键是明确二次根式的混合运算的计算方法,会估算无理数的大小.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
18.下列计算正确的是( )
| A. | (-2a2)3=8a6 | B. | a3÷a2=a | C. | 2a2+a2=3a4 | D. | (a-b)2=a2-b2 |
15.某造纸厂生产甲、乙两种生活用纸的相关信息如下表,其中x(吨)表示甲、乙两种生活用纸的月产量,请根据表中的信息解答后面的问题:
(1)设该造纸厂每月生产甲、乙两种生活用纸的利润分别为y1元和y2元,分别求出y1和y2与x的函数关系式(注:利润=总收入-总支出);
(2)若某月要生产甲、乙两种生活用纸共300吨,求该月生产甲、乙两种生活用纸各多少吨,获得的总利润最大?最大利润是多少?
| 种 品 价 目 | 出厂价(元/吨) | 成本价(元/吨) | 排污处理费 |
| 甲种生活用纸 | 4800 | 2200 | 200(元/吨) 每月还需支付设备管理、 维护费20000元 |
| 乙种生活用纸 | 7000-10x | 1600 | 400(元/吨) |
(2)若某月要生产甲、乙两种生活用纸共300吨,求该月生产甲、乙两种生活用纸各多少吨,获得的总利润最大?最大利润是多少?
2.函数y=-$\frac{6}{x}$的图象经过点A(x1,y1)、B(x2,y2),若x1<x2<0,则y1、y2、0三者的大小关系是( )
| A. | y1<y2<0 | B. | y2<y1<0 | C. | y1>y2>0 | D. | y2>y1>0 |
19.某天的最高气温是11℃,最低气温是-1℃,则这一天的最高气温与最低气温的差是( )
| A. | 2℃ | B. | -2℃ | C. | 12℃ | D. | -12℃ |
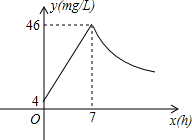 近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如下图,根据题中相关信息回答下列问题:
近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如下图,根据题中相关信息回答下列问题: