题目内容
17．
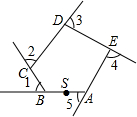如图，五边形ABCDE是一块草地．小明从点S出发，沿着这个五边形的边步行一周，最后仍回到起点S处，小明在各拐弯处转过的角度之和是360°．
分析 根据多边形外角和为360°进行解答．
解答 解：根据多边形外角和公式可得∠1+∠2+∠3+∠4+∠5=360°，
故答案为：360．
点评 此题主要考查了多边形的外角，关键是掌握多边形的外角和等于360度．
练习册系列答案
相关题目
7．
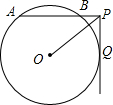如图，⊙O中，点P是弦AB延长线上的一点，连接OP，过P作PQ⊥AP，且与⊙O相切于Q，若OP=4，∠APO=30°，则PA的长是（ ）
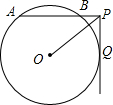如图，⊙O中，点P是弦AB延长线上的一点，连接OP，过P作PQ⊥AP，且与⊙O相切于Q，若OP=4，∠APO=30°，则PA的长是（ ）| A． | 2$\sqrt{3}$+2$\sqrt{2}$ | B． | $\sqrt{5}$ | C． | 2$\sqrt{13}$ | D． | $\sqrt{13}$ |
8．一次函数y=x-2的图象经过点（ ）
| A． | （-2，0） | B． | （0，0） | C． | （0，2） | D． | （0，-2） |
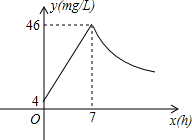近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO．在一次矿难事件的调查中现：从零时起，井内空气中CO的浓度达到4mg/L，此后浓度呈直线型增加，在第7小时达到最高值46mg/L，发生爆炸；爆炸后，空气中的CO浓度成反比例下降．如下图，根据题中相关信息回答下列问题：
2．函数y=-$\frac{6}{x}$的图象经过点A（x1，y1）、B（x2，y2），若x1＜x2＜0，则y1、y2、0三者的大小关系是（ ）
| A． | y1＜y2＜0 | B． | y2＜y1＜0 | C． | y1＞y2＞0 | D． | y2＞y1＞0 |
6．
如图，所示的几何体的正视图是（ ）
如图，所示的几何体的正视图是（ ）| A． |  | B． |  | C． |  | D． |  |