题目内容
7.某校七年级组准备购买一批笔记本奖励优秀学生,在购买时发现,每本笔记本可以打九折,用360元钱购买的笔记本,打折后购买的数量比打折前多10本.(1)求打折前每本笔记本的售价是多少元?
(2)由于考虑学生需求的不同,学校决定购买笔记本和笔袋共90件,笔袋每个原售价为6元,两种物品都打九折,若购买总金额不超过369元,则笔记本至少要买多少本?
分析 (1)设打折前售价为x元,则打折后售价为0.9x元,表示出打折前购买的数量及打折后购买的数量,再由打折后购买的数量比打折前多10本,可得出方程,解出即可.
(2)设购买笔记本y件,则购买笔袋(90-y)件,根据购买总金额不低于360元,且不超过369元,可得出不等式组,解出即可.
解答 (1)解:设打折前售价为x元,则打折后售价为0.9x元,
由题意得,$\frac{360}{x}$+10=$\frac{360}{0.9x}$,
解得:x=4,
经检验得:x=4是原方程的解,
答:打折前每本笔记本的售价为4元.
(2)设购买笔记本y件,则购买笔袋(90-y)件,
由题意得,360≤4×0.9×y+6×0.9×(90-y)≤369,
解得:65≤y≤70,
∵y为正整数,
∴y可取65,66,6768,69,70,
∴y最小为65,
答:笔记本至少要买65本.
点评 此题主要考查了分式方程的应用,一元一次不等式组的应用,解答此类应用类题目,一定要先仔细审题,有时需要读上几遍,找到解题需要的等量关系或不等关系,列出方程或不等式,注意分式方程必须检验.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.若点M(1-m,2+m)在第四象限,则m的取值范围是( )
| A. | m<1 | B. | m>-2 | C. | m<-2 | D. | -2<m<1 |
16.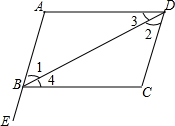 如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
 如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠C=∠CBE | D. | ∠C+∠ABC=180° |
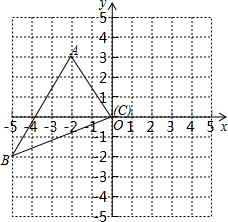 △ABC的位置如图所示:
△ABC的位置如图所示: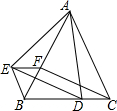 如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF. 如图,点A(0,2),B(-3,1),C(-2,-2).三角形ABC内任意一点P(x0,y0)经过平移后对应点为P1(x0+4,y0-1),将三角形ABC作同样的平移得到三角形A1B1C1;
如图,点A(0,2),B(-3,1),C(-2,-2).三角形ABC内任意一点P(x0,y0)经过平移后对应点为P1(x0+4,y0-1),将三角形ABC作同样的平移得到三角形A1B1C1; 如图,△ABC的三个顶点和点O都在正方形网格的格点上,每个小正方形的边长都为1.
如图,△ABC的三个顶点和点O都在正方形网格的格点上,每个小正方形的边长都为1.