题目内容
2.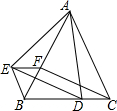 如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
分析 (1)欲证明△ABE≌△ACD只要证明∠EAB=∠CAD,AB=AC,∠EBA=∠ACD即可.
(2)欲证明四边形EFCD是平行四边形,只要证明EF∥CD,EF=CD即可.
解答 证明:(1)∵△ABC和△BEF都是等边三角形,
∴AB=AC,∠EBF=∠ACB=∠BAC=60°,
∵∠EAD=60°,
∴∠EAD=∠BAC,
∴∠EAB=∠CAD,
在△ABE和△ACD中,
$\left\{\begin{array}{l}{∠EBA=∠ACB}\\{AB=AC}\\{∠EAB=∠DAC}\end{array}\right.$,
∴△ABE≌△ACD.
(2)由(1)得△ABE≌△ACD,
∴BE=CD,
∵△BEF、△ABC是等边三角形,
∴BE=EF,
∴∠EFB=∠ABC=60°,
∴EF∥CD,
∴BE=EF=CD,
∴EF=CD,且EF∥CD,
∴四边形EFCD是平行四边形.
点评 本题考查平行四边形的判定和性质、等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,灵活应用平行四边形的判定方法,属于中考常考题型.

练习册系列答案
相关题目
13.下列方程中变形正确的是( )
①3x+6=0变形为x+2=0;
②2x+8=5-3x变形为x=3;
③$\frac{x}{2}+\frac{x}{3}$=4去分母的3x+2x=24;
④(x+2)-2(x-1)=0去括号得x+2-2x-2=0.
①3x+6=0变形为x+2=0;
②2x+8=5-3x变形为x=3;
③$\frac{x}{2}+\frac{x}{3}$=4去分母的3x+2x=24;
④(x+2)-2(x-1)=0去括号得x+2-2x-2=0.
| A. | ①③ | B. | ①②③ | C. | ①④ | D. | ①③④ |
10.为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:那么关于这10户居民月用电量,下列说法错误的是( )
| 居民(户) | 1 | 2 | 3 | 4 |
| 月用电量(度/户) | 30 | 42 | 50 | 51 |
| A. | 中位数是50 | B. | 众数是51 | C. | 极差是21 | D. | 方差是42 |
14. 平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
 平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )| A. | 61° | B. | 63° | C. | 65° | D. | 67° |
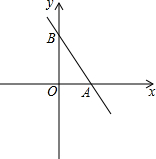 如图,一次函数y=-2x+2的直线与x轴、y轴分别交于A、B两点.
如图,一次函数y=-2x+2的直线与x轴、y轴分别交于A、B两点.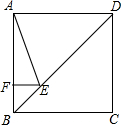 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于点F,求EF的长.
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于点F,求EF的长. 如图,在正方形ABCD中,以CD为边向外作等边三角形CDE,连结AE、BE,则∠AEB=30°.
如图,在正方形ABCD中,以CD为边向外作等边三角形CDE,连结AE、BE,则∠AEB=30°.