题目内容
19.已知a=$\sqrt{3}+\sqrt{5}$,b=$\sqrt{3}-\sqrt{5}$,则ab=-2.分析 根据a=$\sqrt{3}+\sqrt{5}$,b=$\sqrt{3}-\sqrt{5}$,利用平方差公式可以求得ab的值.
解答 解:∵a=$\sqrt{3}+\sqrt{5}$,b=$\sqrt{3}-\sqrt{5}$,
∴ab=$(\sqrt{3}+\sqrt{5})(\sqrt{3}-\sqrt{5})$=3-5=-2,
故答案为:-2.
点评 本题考查二次根式的化简求值,解题的关键是找出所求式子与已知式子之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:那么关于这10户居民月用电量,下列说法错误的是( )
| 居民(户) | 1 | 2 | 3 | 4 |
| 月用电量(度/户) | 30 | 42 | 50 | 51 |
| A. | 中位数是50 | B. | 众数是51 | C. | 极差是21 | D. | 方差是42 |
14. 平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
 平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )
平行四边形ABCD中,对角线AC与BD交于点O,∠DAC=42°,∠CBD=23°,则∠COD是( )| A. | 61° | B. | 63° | C. | 65° | D. | 67° |
4.下列二次根式中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{0.3}$ | B. | $\sqrt{24}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{18}$ |
9.要判断命题“若a>b,则a2>b2”是假命题,可举得反例是( )
| A. | a=1,b=-2 | B. | a=1,b=0 | C. | a=2,b=1 | D. | a=2,b=-1 |
 如图所示,△ABD≌△ACD,∠BAC=90°.
如图所示,△ABD≌△ACD,∠BAC=90°.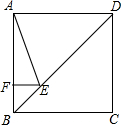 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于点F,求EF的长.
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB于点F,求EF的长.