题目内容
 如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,若将△ABC绕着点C逆时针旋转90°得△EDC.
如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,若将△ABC绕着点C逆时针旋转90°得△EDC.(1)求证:∠ADC+∠CDE=180°;
(2)若AB=3cm,AC=4
| 2 |
(3)在(2)的条件下,求四边形ABCD的周长和面积.
考点:全等三角形的判定与性质,勾股定理,旋转的性质
专题:
分析:(1)通过旋转的性质和四边形内角和定理证得结论;
(2)根据旋转的性质得到AC=EC,AB=ED;然后在等腰直角△ACE中,由勾股定理求得AE的长度,则AD=AE-EC=AE-AB;
(3)如图,连接BD;在(2)的条件下,利用勾股定理可以求得BD的长度,则利用等腰直角三角形的性质易求BC的长度,从而求得四边形ABCD的周长;四边形ABCD的面积=△ACE的面积.
(2)根据旋转的性质得到AC=EC,AB=ED;然后在等腰直角△ACE中,由勾股定理求得AE的长度,则AD=AE-EC=AE-AB;
(3)如图,连接BD;在(2)的条件下,利用勾股定理可以求得BD的长度,则利用等腰直角三角形的性质易求BC的长度,从而求得四边形ABCD的周长;四边形ABCD的面积=△ACE的面积.
解答: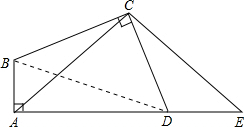 (1)证明:如图,在四边形ABCD中,∠A=∠BCD=90°,则∠B+∠ADC=180°.
(1)证明:如图,在四边形ABCD中,∠A=∠BCD=90°,则∠B+∠ADC=180°.
∵将△ABC绕着点C逆时针旋转90°得△EDC,
∴△ABC≌△EDC,
∴∠CDE=∠CBA,
∴∠ADC+∠CDE=180°;
(2)解:∵将△ABC绕着点C逆时针旋转90°得△EDC,
∴AC=EC=4
cm,AB=ED=3cm,∠ACE=90°,
∴AE=
AC=8cm,
∴AD=AE-EC=AE-AB=5cm;
(3)解:如图,连接BD.
由(2)知,AD=5cm.
则在直角△ABD中,由勾股定理得到:BD=
=
.
又∵BC=CD,∠BCD=90°,
∴BC=CD=
=
,
∴四边形ABCD的周长为:AB+AD+2BC=3+5+2
=8+2
;
∵△ABC≌△EDC,
∴四边形ABCD的面积=△ACE的面积=
AC•CE=
×4
×4
=16(cm2).
综上所述,四边形ABCD的周长为(8+2
)cm,面积为16cm2.
 (1)证明:如图,在四边形ABCD中,∠A=∠BCD=90°,则∠B+∠ADC=180°.
(1)证明:如图,在四边形ABCD中,∠A=∠BCD=90°,则∠B+∠ADC=180°.∵将△ABC绕着点C逆时针旋转90°得△EDC,
∴△ABC≌△EDC,
∴∠CDE=∠CBA,
∴∠ADC+∠CDE=180°;
(2)解:∵将△ABC绕着点C逆时针旋转90°得△EDC,
∴AC=EC=4
| 2 |
∴AE=
| 2 |
∴AD=AE-EC=AE-AB=5cm;
(3)解:如图,连接BD.
由(2)知,AD=5cm.
则在直角△ABD中,由勾股定理得到:BD=
| AB2+AD2 |
| 34 |
又∵BC=CD,∠BCD=90°,
∴BC=CD=
| ||
|
| 17 |
∴四边形ABCD的周长为:AB+AD+2BC=3+5+2
| 17 |
| 17 |
∵△ABC≌△EDC,
∴四边形ABCD的面积=△ACE的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
综上所述,四边形ABCD的周长为(8+2
| 17 |
点评:本题考查了全等三角形的判定与性质,旋转的性质以及三角形的面积.旋转前、后的图形全等.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,则正确的结论是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,则正确的结论是( )| A、abc>0 |
| B、3a+c<0 |
| C、4a+2b+c<0 |
| D、b2-4ac<0 |
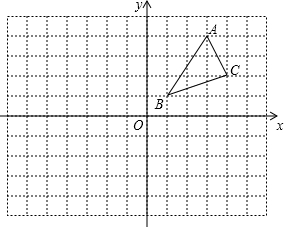 如图,点C的坐标为(4,2),作出△ABC关于y轴对称的图形△A1B1C1,再作出△A1B1C1关于原点对称的△A2B2C2,并写出点A2、B2、C2的坐标.
如图,点C的坐标为(4,2),作出△ABC关于y轴对称的图形△A1B1C1,再作出△A1B1C1关于原点对称的△A2B2C2,并写出点A2、B2、C2的坐标. 如图,小方格的边长都是1,求五边形ABCDE的周长和面积?
如图,小方格的边长都是1,求五边形ABCDE的周长和面积?
 如图,点B、C为线段AD上两点,BC=5cm,点E为AB的中点,点F为CD的中点,EF=7cm,求线段AD的长.
如图,点B、C为线段AD上两点,BC=5cm,点E为AB的中点,点F为CD的中点,EF=7cm,求线段AD的长.