题目内容
17.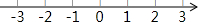 解不等式组:$\left\{\begin{array}{l}{1+x>-2,}&{①}\\{\frac{2x-1}{3}≤1,}&{②}\end{array}\right.$.请结合题意填空,完成本题的解答.
解不等式组:$\left\{\begin{array}{l}{1+x>-2,}&{①}\\{\frac{2x-1}{3}≤1,}&{②}\end{array}\right.$.请结合题意填空,完成本题的解答.(Ⅰ)解不等式①,得x>-3;
(Ⅱ)解不等式②,得x≤2;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为-3<x≤2.
分析 根据不等式基本性质分别求出不等式①、②的解集,由大于向右、小于向左,包括该数用实心点、不包括该数用空心点在数轴上表示不等式的解集,结合解集找到其公共部分即可得不等式组的解集.
解答 解:$\left\{\begin{array}{l}{1+x>-2,}&{①}\\{\frac{2x-1}{3}≤1,}&{②}\end{array}\right.$,
(Ⅰ)解不等式①得:x>-3,
(Ⅱ)解不等式②得:x≤2,
(Ⅲ)把不等式①和②的解集在数轴上表示出来如图:
(Ⅳ)原不等式组的解集为:-3<x≤2,
故答案为:(Ⅰ)x>-3;(Ⅱ)x≤2;(Ⅳ)-3<x≤2.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集,并将解集表示在数轴上找到其公共部分是关键.

练习册系列答案
相关题目
9. 某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
请根据图表信息解答下列问题:
(1)本次共抽样调查120个学生;
(2)填空:频数分布表中的m=30,n=0.3;
(3)在扇形统计图中,请计算出“摩托车”所在的扇形的圆心角的度数.
 某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 交通方式 | 频数(人数) | 频率 |
| 公共汽车 | m | 0.25 |
| 小车 | 24 | 0.20 |
| 摩托车 | 36 | n |
| 自行车 | 18 | 0.15 |
| 其它 | 12 | 0.10 |
(1)本次共抽样调查120个学生;
(2)填空:频数分布表中的m=30,n=0.3;
(3)在扇形统计图中,请计算出“摩托车”所在的扇形的圆心角的度数.
1.已知x+y=7,xy=-8,下列各式计算结果不正确的是( )
| A. | (x-y)2=81 | B. | x2+y2=65 | C. | x2+y2-xy=71 | D. | x2-y2=±63 |
 直线l1∥l2,一块含45°角的直角三角板如图放置,∠1=89°,则∠2=44°.
直线l1∥l2,一块含45°角的直角三角板如图放置,∠1=89°,则∠2=44°.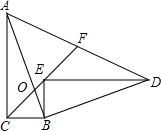 如图,在Rt△ABC中,∠ACB=90°,sin∠CAB=$\frac{1}{3}$,点O在AB上,且CB=CO=3,若Rt△ABC绕点B顺时针旋转一定角度后得到Rt△BED,且E落在CO的延长线上,连接AD交CO的延长线于F,则AF的长为7.
如图,在Rt△ABC中,∠ACB=90°,sin∠CAB=$\frac{1}{3}$,点O在AB上,且CB=CO=3,若Rt△ABC绕点B顺时针旋转一定角度后得到Rt△BED,且E落在CO的延长线上,连接AD交CO的延长线于F,则AF的长为7. 看图填空:
看图填空: