题目内容
8.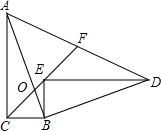 如图,在Rt△ABC中,∠ACB=90°,sin∠CAB=$\frac{1}{3}$,点O在AB上,且CB=CO=3,若Rt△ABC绕点B顺时针旋转一定角度后得到Rt△BED,且E落在CO的延长线上,连接AD交CO的延长线于F,则AF的长为7.
如图,在Rt△ABC中,∠ACB=90°,sin∠CAB=$\frac{1}{3}$,点O在AB上,且CB=CO=3,若Rt△ABC绕点B顺时针旋转一定角度后得到Rt△BED,且E落在CO的延长线上,连接AD交CO的延长线于F,则AF的长为7.
分析 先由旋转的性质,判断出△BCE∽△BAD,得出结论再判断出△BOC∽△FOA,再用锐角三角函数求解即可
解答 解:如图,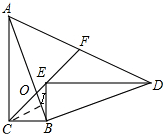
由旋转得,∠ABC=∠DBE,BC=BE,BA=BD,
∴∠CBE=∠ABD,
∴△BCE∽△BAD,
∴∠BCE=∠BAD,
∵∠COB=∠AOF,
∴△BOC∽FOA,
∵OC=BC=3,
∴AO=AF.
作CI⊥AB,
∴∠BCI=∠BAC,BI=OI,
∴sin∠BCI=$\frac{BI}{BC}=\frac{BI}{3}$=sin∠BAC=$\frac{1}{3}$,
∴AB=9,BI=1=OI,BO=2,
∴AF=AO=AB-BO=7.
故答案为7.
点评 此题是旋转的性质题,主要考查了相似三角形的性质和判定,锐角三角函数的意义,旋转的性质,解本题的关键是锐角三角函数的意义的应用.

练习册系列答案
相关题目
18.下列选项是无理数的为( )
| A. | -$\frac{1}{3}$ | B. | $\sqrt{4}$ | C. | 3.1415926 | D. | -π |
19.点A(-4,0)与点B(4,0)是( )
| A. | 关于y轴对称 | B. | 关于x轴对称 | ||
| C. | 关于坐标轴都对称 | D. | 以上答案都错 |
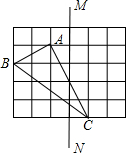 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题. 如图,四边形ABCD是平行四边形.
如图,四边形ABCD是平行四边形. 解不等式组:$\left\{\begin{array}{l}{1+x>-2,}&{①}\\{\frac{2x-1}{3}≤1,}&{②}\end{array}\right.$.请结合题意填空,完成本题的解答.
解不等式组:$\left\{\begin{array}{l}{1+x>-2,}&{①}\\{\frac{2x-1}{3}≤1,}&{②}\end{array}\right.$.请结合题意填空,完成本题的解答.