题目内容
3.在矩形ABCD中,∠A和∠B的平分线交边CD于点M和N.若M、N是CD的三等分点.那么AB:BC的值为3:1或3:2.分析 分两种情形:①如图1中,只要证明AD=DM=MN=NC=BC即可解决问题,②如图2中,只要证明AD=DM=MN=NC=BC即可解决问题.
解答 解:如图1中,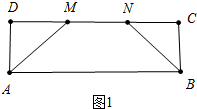
∵四边形ABCD是矩形,
∴AB∥CD,∠DAB=∠ABC=90°,AB=CD,AD=CB,
∵AM平分∠DAB,NB平分∠ABC,
∴∠DAM=∠MAB=∠AMD=45°,∠CBN=∠ABN=∠CNB=45°,
∴AD=DM,CN=BC,
∵DM=MN=NC,
∴AB:BC=3:1.
如图2中,
∵四边形ABCD是矩形,
∴AB∥CD,∠DAB=∠ABC=90°,AB=CD,AD=CB,
∵AM平分∠DAB,NB平分∠ABC,
∴∠DAM=∠MAB=∠AMD=45°,∠CBN=∠ABN=∠CNB=45°,
∴AD=DM,CN=BC,
∵DN=NM=MC,
∴AB:BC=3:2.
点评 本题考查矩形的性质、等腰三角形的判定和性质等知识,解题的关键是等腰直角三角形的证明,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.比较2,$\sqrt{5}$,$\root{3}{7}$的大小,正确的是( )
| A. | 2<$\sqrt{5}$<$\root{3}{7}$ | B. | 2<$\root{3}{7}$<$\sqrt{5}$ | C. | $\sqrt{5}$<$\root{3}{7}$<2 | D. | $\root{3}{7}$<2<$\sqrt{5}$ |
11.下列事件:(1)如果x、y都是实数,那么x+y=y+x;(2)从分别标有数字1~10的10张小标签中任取1张,得到6号签;(3)同时抛掷两枚骰子,向上一面的点数之积为28;(4)设计1次,中靶,其中随机事件的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
15.下列运算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | (a+b)2=a2+b2 | C. | (-a)3=-6a3 | D. | -(x-2)=2-x |
13.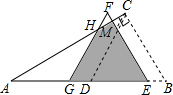 如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.
如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.
 如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.
如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.| A. | $\frac{7\sqrt{3}}{8}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
 如图,在矩形ABCD中,AD=3,AB=4,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对点D′落在矩形的对角线上,DE的长为1.5或$\frac{9}{4}$.
如图,在矩形ABCD中,AD=3,AB=4,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对点D′落在矩形的对角线上,DE的长为1.5或$\frac{9}{4}$.