题目内容
8. 如图,在矩形ABCD中,AD=3,AB=4,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对点D′落在矩形的对角线上,DE的长为1.5或$\frac{9}{4}$.
如图,在矩形ABCD中,AD=3,AB=4,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对点D′落在矩形的对角线上,DE的长为1.5或$\frac{9}{4}$.
分析 先依据勾股定理可求得AC的长,然后由翻折的性质可求得AD=AD′=3,于是可求得D′C的长,接下来,证明△ECD′∽△ADC,依据相似三角形的性质可求得ED′=1.5,由翻折的性质可求得DE的长.
解答 解:如图所示;连接AC.
∵由翻折的性质可知;DE=ED′,AD=AD′=3,∠D=∠ED′A=90°,
∴∠ED′C=90°.
∵在△ABC中,由勾股定理得:AC=$\sqrt{B{C}^{2}+A{B}^{2}}$=5.
∴CD′=AC-AD′=2.
∵∠ECD′=∠DCA,∠ED′C=∠CDA=90°,
∴△ECD′∽△ADC.
∴$\frac{D′C}{DC}=\frac{ED′}{AD}$即$\frac{2}{4}=\frac{ED′}{3}$,解得;ED′=1.5.
∴DE=1.5.
如图所示:
∵∠ADO+∠DAO=90°,∠ADB+∠ABD=90°,
∴∠DAO=∠DBA.
∴OD=AD×$\frac{3}{5}$=$\frac{9}{5}$.
∴DE=OD÷$\frac{4}{5}$=$\frac{9}{5}$×$\frac{5}{4}$=$\frac{9}{4}$.
故答案为:1.5或$\frac{9}{4}$.
点评 本题主要考查的是翻折的性质、勾股定理、相似三角形的性质和判定,依据相似三角形的性质求得ED′的长是解题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
18.已知命题:若a>b,则$\frac{1}{a}<\frac{1}{b}$.下列哪个反例可以说明这是个假命题( )
| A. | a=2,b=1 | B. | a=2,b=-1 | C. | a=1,b=2 | D. | a=-2,b=-1 |
19.x取( )时,式子$\frac{\sqrt{x-2}}{x-1}$在实数范围内有意义.
| A. | x≥1且x≠2 | B. | x≥2且x≠1 | C. | x≥2 | D. | 都不正确 |
17.下列代数式运算正确的是( )
| A. | (x3)2=x5 | B. | x3•x2=x5 | C. | (2x)2=2x2 | D. | (x+2)2=x2+2 |
18.已知点(-5,y1)、(-3,y2)都在直线y=-8x+7上,则y1、y2的大小关系为( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法比较 |
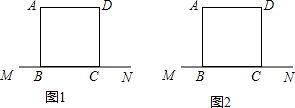 已知正方形ABCD如图所示,M、N在直线BC上,MB=NC,试分别在图1、图2中仅用无刻度的直尺画出一个不同的等腰三角形OMN.
已知正方形ABCD如图所示,M、N在直线BC上,MB=NC,试分别在图1、图2中仅用无刻度的直尺画出一个不同的等腰三角形OMN. 如图,直线l1与直线l2互相垂直,A,B是两个定点.C,D分别是直线l1,l2上的动点.试确定C,D两点的位置,使四边形ACDB的周长最短.
如图,直线l1与直线l2互相垂直,A,B是两个定点.C,D分别是直线l1,l2上的动点.试确定C,D两点的位置,使四边形ACDB的周长最短.