题目内容
13.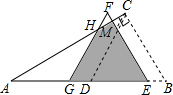 如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.
如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.| A. | $\frac{7\sqrt{3}}{8}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 过C作CN⊥AB于N,证明△BCD为等边三角形,利用含30°角的直角三角形的性质计算出CN,MF,HM,再表示出△FHM和△FGE的面积,求差即可.
解答 解:如图:过C作CN⊥AB于N,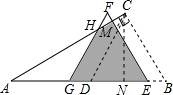 ∵△ABC中,∠ACB=90°,∠CAB=30°,
∵△ABC中,∠ACB=90°,∠CAB=30°,
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2.
∵△ABC中,∠ACB=90°,D是AB的中点,
∴CD=BD=AD=2,
∵∠ABC=60°,
∴△BCD为等边三角形,
∴NB=$\frac{1}{2}$BD=1,CN=$\sqrt{3}$NB=$\sqrt{3}$,
∵DG=1,AD=2,
∴GH=AG=1,
∴FH=1,
∵∠A=30°,
∴∠A=30°=∠AHG=∠FHM=30°,
∵FE∥CB,∠ACB=90°,
∴MF=$\frac{1}{2}$FH=$\frac{1}{2}$,HM=$\sqrt{3}$FM=$\frac{\sqrt{3}}{2}$.
∴S△EFG=S△BCD=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
S△MFH=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{8}$,
∴S四边形GHME=$\sqrt{3}$-$\frac{\sqrt{3}}{8}$=$\frac{7\sqrt{3}}{8}$(cm2).
即△EFG与△ABC重叠部分的面积为$\frac{7\sqrt{3}}{8}$cm2.
故选A.
点评 此题考查了平移的性质,含30°角的直角三角形的性质,等边三角形的判定与性质,平行线的性质,关键是准确作出辅助线.

练习册系列答案
相关题目
1.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (ab)2=a2b2 | C. | (a2)3=a5 | D. | a2+2a2=3a4 |
8.已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax-3y=1}\\{x+by=5}\end{array}\right.$的解,则a,b的值分别是( )
| A. | 3,2 | B. | 2,3 | C. | -3,2 | D. | -2,3 |
18.已知点(-5,y1)、(-3,y2)都在直线y=-8x+7上,则y1、y2的大小关系为( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 无法比较 |
20.针对娄底市城区中小学日益突出的“大班额”问题,娄底市自2012年起,启动《中心城区化解大班额四年(2012-2015)行动计划》,计划投入资金871000000元,力争新增学位3.29万个.计划投入资金871000000元这个数据用科学记数法(保留2个有效数字)表示为( )
| A. | 8.7×106元 | B. | 8.71×106元 | C. | 8.7×108元 | D. | 8.71×108元 |
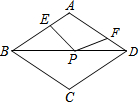 如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )
如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )