题目内容
19.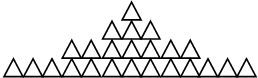 如图:由三角形摆成的图案;摆第1层需一个三角形,摆第2层需要3个三角形;摆第3层需要7个三角形,摆第4层需要13个三角形,摆第5层需要21个三角形…摆到第n层需要n2-n+1个三角形.
如图:由三角形摆成的图案;摆第1层需一个三角形,摆第2层需要3个三角形;摆第3层需要7个三角形,摆第4层需要13个三角形,摆第5层需要21个三角形…摆到第n层需要n2-n+1个三角形.
分析 观察可得,第1层三角形的个数为1,第2层三角形的个数为3,比第1层多2个;第3层三角形的个数为7,比第2层多4个;…可得,每一层比上一层多的个数依次为2,4,6,…据此作答.
解答 解:观察可得,第1层三角形的个数为1,第2层三角形的个数为22-2+1=3,
第3层三角形的个数为32-3+1=7,
第四层图需要42-4+1=13个三角形
摆第五层图需要52-5+1=21.
那么摆第n层图需要n2-n+1个三角形.
故答案为:21;n2-n+1.
点评 此题考查了平面图形的有规律变化,要求学生通过观察图形,分析、归纳发现其中的规律,并应用规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.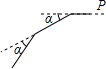 如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
 如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )
如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=( )| A. | 30° | B. | 40° | C. | 80° | D. | 108° |
4.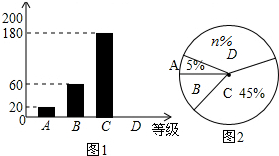 据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
(1)本次参与调查的学生共有400人,m=15%,n=35.
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(3)请补全图1示数的条形统计图;
(4)根据调查结果,学校准备开展关于“剪刀石头布”知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个求上的数字和为奇数,则小明去;否则小刚去,请用树状图或列表法说明这个游戏规则是否公平.
 据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:| 对提议的了解程度 | 百分比 |
| A、非常了解 | 5% |
| B、比较了解 | m |
| C、基本了解 | 45% |
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(3)请补全图1示数的条形统计图;
(4)根据调查结果,学校准备开展关于“剪刀石头布”知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个求上的数字和为奇数,则小明去;否则小刚去,请用树状图或列表法说明这个游戏规则是否公平.
8.某商场为从甲、乙两种电子钟中购入一种去销售.从两种电子钟中各随机取10台进行测试,两种电子钟走时误差的数据如下表.(单位:秒)
(1)计算出甲、乙两种电子钟走时误差的平均数;
(2)计算出甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优,消费者也更愿意购买.若销售一台甲种电子钟和销售一台乙种电子钟的利润相同,请问:商场应购入哪种电子钟去销售,为什么?
类型 编号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
| 甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
| 乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(2)计算出甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优,消费者也更愿意购买.若销售一台甲种电子钟和销售一台乙种电子钟的利润相同,请问:商场应购入哪种电子钟去销售,为什么?
 如图,将△ABC沿水平向右的方向平移,得到△EAF,若AB=5,BC=3,AC=4,则平移的距离是( )
如图,将△ABC沿水平向右的方向平移,得到△EAF,若AB=5,BC=3,AC=4,则平移的距离是( )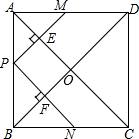 如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论: 如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2=34°.
如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2=34°. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E 交AC于F,若AB=10,BC=7,AC=8,则△AEF的周长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线交于点D,过点D作EF∥BC交AB于E 交AC于F,若AB=10,BC=7,AC=8,则△AEF的周长为( )