题目内容
8.某商场为从甲、乙两种电子钟中购入一种去销售.从两种电子钟中各随机取10台进行测试,两种电子钟走时误差的数据如下表.(单位:秒)类型 编号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
| 甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
| 乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(2)计算出甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优,消费者也更愿意购买.若销售一台甲种电子钟和销售一台乙种电子钟的利润相同,请问:商场应购入哪种电子钟去销售,为什么?
分析 根据平均数与方差的计算公式易得(1)(2)的答案,再根据(2)的计算结果进行判断.
解答 解:(1)甲种电子钟走时误差的平均数是:$\frac{1}{10}$(1-3-4+4+2-2+2-1-1+2)=0,
乙种电子钟走时误差的平均数是:$\frac{1}{10}$(4-3-1+2-2+1-2+2-2+1)=0.
(2)S2甲=$\frac{1}{10}$[(1-0)2+(-3-0)2+…+(2-0)2]=$\frac{1}{10}$×60=6(s2),
S2乙=$\frac{1}{10}$[(4-0)2+(-3-0)2+…+(1-0)2]=$\frac{1}{10}$×48=4.8(s2),
故甲乙两种电子钟走时误差的方差分别是6s2和4.8s2;
(3)商场应购入乙种电子钟,因为两种类型的电子钟利润相同,且甲的方差比乙的大,说明乙的稳定性更好,故乙种电子钟的质量更优.
点评 本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.同时考查平均数公式:$\overline{x}$=$\frac{{x}_{1}+{x}_{2}+…+{x}_{n}}{n}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
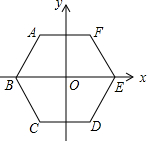 如图,正六边形ABCDEF的边长为2,它的中心与坐标原点O重合,对角线BE在x轴上,若抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的三个顶点,则该抛物线的解析式为y=$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x-$\frac{2\sqrt{3}}{3}$.
如图,正六边形ABCDEF的边长为2,它的中心与坐标原点O重合,对角线BE在x轴上,若抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的三个顶点,则该抛物线的解析式为y=$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x-$\frac{2\sqrt{3}}{3}$.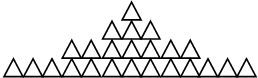 如图:由三角形摆成的图案;摆第1层需一个三角形,摆第2层需要3个三角形;摆第3层需要7个三角形,摆第4层需要13个三角形,摆第5层需要21个三角形…摆到第n层需要n2-n+1个三角形.
如图:由三角形摆成的图案;摆第1层需一个三角形,摆第2层需要3个三角形;摆第3层需要7个三角形,摆第4层需要13个三角形,摆第5层需要21个三角形…摆到第n层需要n2-n+1个三角形.

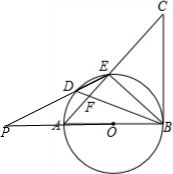 如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,且∠BDE=∠CBE,BD与AE交于点F.
如图,AB是⊙O的直径,点D是$\widehat{AE}$上一点,且∠BDE=∠CBE,BD与AE交于点F.