题目内容
9. 如图,将△ABC沿水平向右的方向平移,得到△EAF,若AB=5,BC=3,AC=4,则平移的距离是( )
如图,将△ABC沿水平向右的方向平移,得到△EAF,若AB=5,BC=3,AC=4,则平移的距离是( )| A. | 3 | B. | 4 | C. | 5 | D. | 10 |
分析 利用勾股定理得逆定理得出△ABC是Rt△,进而利用平移的性质和勾股定理求出FC的长,即可得出答案.
解答 解:∵AB=5,BC=3,AC=4,
∴AB2=BC2+AC2,
∴△ABC是Rt△,
∵将△ABC沿水平向右的方向平移,得到△EAF,
∴AC=4,AF=3,∠CAF=90°,
∴FC=$\sqrt{{3}^{2}+{4}^{2}}$=5.
故选:C.
点评 此题主要考查了平移的性质以及勾股定理和勾股定理的逆定理,得出∠CAF=90°是解题关键.

练习册系列答案
相关题目
20.解方程$\frac{4}{4-2x}$=$\frac{2}{2-x}$的结果是( )
| A. | x=-2 | B. | x=2 | C. | x=4 | D. | x≠2 |
 如图,矩形内有两个面积分别是4和9的正方形,则图中阴影部分的面积是2.
如图,矩形内有两个面积分别是4和9的正方形,则图中阴影部分的面积是2. 如图,已知△AOC≌△BOC,∠A=100°,则∠B=100°.
如图,已知△AOC≌△BOC,∠A=100°,则∠B=100°.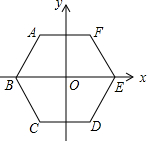 如图,正六边形ABCDEF的边长为2,它的中心与坐标原点O重合,对角线BE在x轴上,若抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的三个顶点,则该抛物线的解析式为y=$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x-$\frac{2\sqrt{3}}{3}$.
如图,正六边形ABCDEF的边长为2,它的中心与坐标原点O重合,对角线BE在x轴上,若抛物线y=ax2+bx+c(a>0,b>0)经过正六边形的三个顶点,则该抛物线的解析式为y=$\frac{2\sqrt{3}}{3}$x2+$\sqrt{3}$x-$\frac{2\sqrt{3}}{3}$.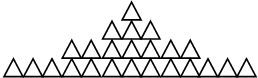 如图:由三角形摆成的图案;摆第1层需一个三角形,摆第2层需要3个三角形;摆第3层需要7个三角形,摆第4层需要13个三角形,摆第5层需要21个三角形…摆到第n层需要n2-n+1个三角形.
如图:由三角形摆成的图案;摆第1层需一个三角形,摆第2层需要3个三角形;摆第3层需要7个三角形,摆第4层需要13个三角形,摆第5层需要21个三角形…摆到第n层需要n2-n+1个三角形.