题目内容
2.若k>-1,则关于x的方程2x2-(4k+1)x+2k2-1=0的根的情况是( )| A. | 方程有两个相等的实数根 | B. | 方程没有实数根 | ||
| C. | 方程有两个不相等的实数根 | D. | 无法判断 |
分析 由方程的系数结合根的判别式得出△=8k+9,再由k>-1即可得出△>1,从而即可得出结论.
解答 解:由已知得:
△=[-(4k+1)]2-4×2×(2k2-1)=8k+9.
∵k>-1,
∴△=8k+9>1,
∴该方程有两个不相等的实数根.
故选C.
点评 本题考查了根的判别式,解题的关键是找出△的正负.本题属于基础题,难度不大,解决该题型题目时,利用根的判别式的符号来确定方程解得个数是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.计算:
(1)(-x2y5)•(xy)3
(2)4a(a-b+1)
(3)10032(简便计算)
(4)x2-(x+1)(x-1)
(5)先化简再求值:(a-2)2+2(a-1)(a+2),其中a=-2.
(1)(-x2y5)•(xy)3
(2)4a(a-b+1)
(3)10032(简便计算)
(4)x2-(x+1)(x-1)
(5)先化简再求值:(a-2)2+2(a-1)(a+2),其中a=-2.
12.在下列四组线段中,能组成直角三角形的是( )
| A. | a=9 b=12 c=15 | B. | a=32 b=42 c=52 | C. | a=12 b=18 c=22 | D. | a:b:c=1:1:2 |
 如图所示,已知⊙O1与⊙O2相交于A、B两点,直线O1O2交⊙O1于P点,直线PA交⊙O2于C点,直线PB交⊙O2于D点.求证:O1O2⊥CD.
如图所示,已知⊙O1与⊙O2相交于A、B两点,直线O1O2交⊙O1于P点,直线PA交⊙O2于C点,直线PB交⊙O2于D点.求证:O1O2⊥CD.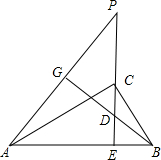 如图在直角三角形△ACB中,∠ACB=90°,CE⊥AB,垂足为E,BG⊥AP,垂足为G,求证:CE2=PE•DE.
如图在直角三角形△ACB中,∠ACB=90°,CE⊥AB,垂足为E,BG⊥AP,垂足为G,求证:CE2=PE•DE.