题目内容
12. 如图所示,已知⊙O1与⊙O2相交于A、B两点,直线O1O2交⊙O1于P点,直线PA交⊙O2于C点,直线PB交⊙O2于D点.求证:O1O2⊥CD.
如图所示,已知⊙O1与⊙O2相交于A、B两点,直线O1O2交⊙O1于P点,直线PA交⊙O2于C点,直线PB交⊙O2于D点.求证:O1O2⊥CD.
分析 根据两圆的连心线垂直平分公共弦,可以证明△PAB是等腰三角形,PO1是角平分线,再证明△PCD是等腰三角形即可解决问题.
解答 证明:如图连接 AB.
AB.
∵O1O2垂直平分AB,
∴PA=PB,∠APO1=∠BPO1
∴∠PAB=∠PBA,
∵∠PAB=∠PDC,∠PBA=∠PCD,
∴∠PDC=∠PCD,
∴PC=PD,
∵∠APO1=∠BPO1,
∴PO2⊥CD.
点评 本题考查圆与圆的位置关系,等腰三角形的判定和性质、圆内接四边形的性质等知识,记住两圆的连心线垂直平分公共弦,属于中考常考题型.

练习册系列答案
相关题目
14. 如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
 如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )| A. | 50° | B. | 60° | C. | 120° | D. | 130° |
15. 实数a,b在数轴上的位置如图所示,则|a|-|b|可化简为( )
实数a,b在数轴上的位置如图所示,则|a|-|b|可化简为( )
 实数a,b在数轴上的位置如图所示,则|a|-|b|可化简为( )
实数a,b在数轴上的位置如图所示,则|a|-|b|可化简为( )| A. | a-b | B. | b-a | C. | a+b | D. | -a-b |
4.2015年双11淘宝全天交易额为571亿,将数字57100000000用科学记数法表示为( )
| A. | 5.71×108 | B. | 5.71×1010 | C. | 5.71×109 | D. | 571×108 |
2.若k>-1,则关于x的方程2x2-(4k+1)x+2k2-1=0的根的情况是( )
| A. | 方程有两个相等的实数根 | B. | 方程没有实数根 | ||
| C. | 方程有两个不相等的实数根 | D. | 无法判断 |
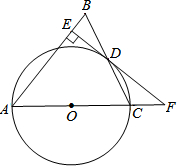 如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.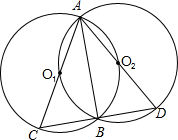 如图,两等圆⊙O1和⊙O2相交于A、B两点,且两圆相互过圆心,过点B作任一直线,分别交⊙O1、⊙O2于C、D两点,接AC、AD.试猜想△ACD的形状,并说明理由.
如图,两等圆⊙O1和⊙O2相交于A、B两点,且两圆相互过圆心,过点B作任一直线,分别交⊙O1、⊙O2于C、D两点,接AC、AD.试猜想△ACD的形状,并说明理由.