题目内容
7.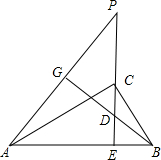 如图在直角三角形△ACB中,∠ACB=90°,CE⊥AB,垂足为E,BG⊥AP,垂足为G,求证:CE2=PE•DE.
如图在直角三角形△ACB中,∠ACB=90°,CE⊥AB,垂足为E,BG⊥AP,垂足为G,求证:CE2=PE•DE.
分析 首先由射影定理,得出CE2=AE•BE,再通过证△AEP∽△BED,得出PE•DE=AE•BE,联立上述两式即可得出结论.
解答  证明:∵∠ACB=90°,CE⊥AB,
证明:∵∠ACB=90°,CE⊥AB,
∴CE2=AE•BE,
∵BG⊥AP,CE⊥AB,
∴∠DEB=∠DGP=∠PEA=90°,
∵∠1=∠2,
∴∠P=∠3,
∴△AEP∽△DEB,
∴$\frac{PE}{BE}$=$\frac{AE}{DE}$,
∴PE•DE=AE•BE,
∴CE2=PE•DE.
点评 此题主要考查了相似三角形的判定和性质、射影定理、三角形内角和定理等知识;熟练掌握相似三角形的判定和性质是解决问题的关键.

练习册系列答案
相关题目
2.若k>-1,则关于x的方程2x2-(4k+1)x+2k2-1=0的根的情况是( )
| A. | 方程有两个相等的实数根 | B. | 方程没有实数根 | ||
| C. | 方程有两个不相等的实数根 | D. | 无法判断 |
12.一辆汽车开往距离出发地180千米的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分钟到达目的地.设前一小时的速度为x千米/小时.则下列方程正确的是( )
| A. | $\frac{180}{x}$-40=$\frac{180-x}{1.5x}$ | B. | $\frac{180}{x}$-40=1+$\frac{180-x}{1.5x}$ | ||
| C. | $\frac{180}{1.5x}$-$\frac{40}{60}$=1+$\frac{180-1.5x}{x}$ | D. | $\frac{180}{x}$-$\frac{40}{60}$=1+$\frac{180-x}{1.5x}$ |
 如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2-4x+a=0的两个实数根.
如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2-4x+a=0的两个实数根.