题目内容
11.四边形ABCD中,AD∥BC,AC交BD于点O.点E、F分别在OA、OB上,作射线DE、CF交AB分别于点M、N.$\frac{∠ODE}{∠ADE}$=$\frac{∠OCF}{∠BCF}$=n.(1)当n=1,AC⊥BD时,①求∠ADO+∠BCO的值;②求∠DEO+∠CFO的值.
(2)当n=2,试探究:∠AMD+∠BNC与∠DOC的数量关系,证明你的结论.
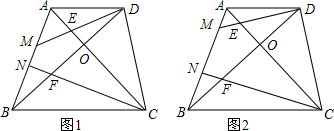
分析 (1)先根据AD∥BC,得出∠ADO=∠OBC.由$\frac{∠ODE}{∠ADE}$=$\frac{∠OCF}{∠BCF}$=1,可设∠ODE=∠ADE=α,∠OCF=∠BCF=β.由AC⊥BD,得出∠OBC+∠BCO=90°,等量代换得出∠ADO+∠BCO=90°;于是2α+2β=90°,即α+β=45°.
再根据直角三角形两锐角互余得出∠DEO=90°-α,∠CFO=90°-β,于是求出∠DEO+∠CFO=90°-α+90°-β=180°-(α+β)=135°;
(2)先根据AD∥BC,得出∠ADO=∠OBC,∠DAB+∠ABC=180°.由$\frac{∠ODE}{∠ADE}$=$\frac{∠OCF}{∠BCF}$=2,可设∠ADE=γ,∠BCF=θ,则∠ODE=2γ,∠OCF=2θ.根据三角形内角和定理得出∠AMD+∠BNC=180°-∠DAB-γ+180°-∠ABC-θ=180°-(γ+θ),根据三角形外角的性质得出∠DOC=∠OBC+∠BCO=∠ADO+∠BCO=3γ+3θ=3(γ+θ),于是得出∠AMD+∠BNC=180°-$\frac{1}{3}$∠DOC.
解答  解:(1)∵AD∥BC,
解:(1)∵AD∥BC,
∴∠ADO=∠OBC.
∵$\frac{∠ODE}{∠ADE}$=$\frac{∠OCF}{∠BCF}$=1,
∴可设∠ODE=∠ADE=α,∠OCF=∠BCF=β.
∵AC⊥BD,
∴∠DOC=90°,
∴∠OBC+∠BCO=90°,
∴∠ADO+∠BCO=90°;
∴2α+2β=90°,
∴α+β=45°.
∵∠DEO=90°-α,∠CFO=90°-β,
∴∠DEO+∠CFO=90°-α+90°-β=180°-(α+β)=135°;
(2)∠AMD+∠BNC=180°-$\frac{1}{3}$∠DOC.理由如下:
∵AD∥BC,
∴∠ADO=∠OBC,∠DAB+∠ABC=180°.
∵$\frac{∠ODE}{∠ADE}$=$\frac{∠OCF}{∠BCF}$=2,
∴可设∠ADE=γ,∠BCF=θ,则∠ODE=2γ,∠OCF=2θ.
∵∠AMD+∠BNC=180°-∠DAB-γ+180°-∠ABC-θ=360°-(∠DAB+∠ABC)-(γ+θ)=180°-(γ+θ),
∠DOC=∠OBC+∠BCO=∠ADO+∠BCO=3γ+3θ=3(γ+θ),
∴∠AMD+∠BNC=180°-$\frac{1}{3}$∠DOC.
点评 本题考查了多边形内角与外角,平行线的性质,三角形内角和定理以及外角的性质,理清各个角之间的关系是解题的关键.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案| A. | 明天会下雨 | |
| B. | 小强期末数学考试会得100分 | |
| C. | 深圳冬天会下雪 | |
| D. | 从一个只装有10个红球的袋子里任意摸出一个刚好是红球 |
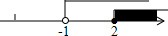 其解集如数轴上所示的不等式组为( )
其解集如数轴上所示的不等式组为( )| A. | $\left\{\begin{array}{l}{x+1≥0}\\{x-2>0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1>0}\\{x-2≥0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+1≤0}\\{2-x<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+1<0}\\{2-x≤0}\end{array}\right.$ |
| A. | (-1,2) | B. | (-1,-2) | C. | (1,2) | D. | (1,-2) |
| A. | x(x-1)=3782 | B. | $\frac{x(x-1)}{2}$=3782 | C. | 2x(x-1)=3782 | D. | x(x+1)=3782 |
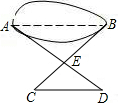 为了测量水塘边A、B两点之间的距离,在可以看到A、B的E处,取AE、BE延长线上的C、D两点,使CD∥AB.如果测量得CD=5米,AD=15米,ED=3米,你能求出AB两点之间的距离吗?
为了测量水塘边A、B两点之间的距离,在可以看到A、B的E处,取AE、BE延长线上的C、D两点,使CD∥AB.如果测量得CD=5米,AD=15米,ED=3米,你能求出AB两点之间的距离吗?