题目内容
15．一个三角形可被分成两个等腰三角形，原三角形的一个内角的36°，则原三角形最大内角的所有可能值为72°或90°或108°或126°或132°．分析 分为以下情况：
①原三角形是锐角三角形，最大角是72°的情况；
②原三角形是直角三角形，最大角是90°的情况；
③原三角形是钝角三角形，最大角是108°的情况；
④原三角形是钝角三角形，最大角是126°的情况；
⑤原三角形是钝角三角形，最大角是132°的情况．
解答 解：①原三角形是锐角三角形，最大角是72°的情况：
如图∠ABC=∠ACB=72°，∠A=36°，AD=BD=BC，则最大角是72°；
，
②原三角形是直角三角形，最大角是90°的情况：
如图∠ABC=90°，∠A=36°，AD=CD=BD，；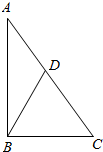
③原三角形是钝角三角形，最大角是108°的情况：
如图∠BAC=108°，∠B=36°，BD=AB，AD=DC，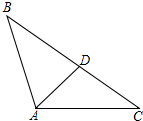
④原三角形是钝角三角形，最大角是126°的情况：
如图∠ABC=126°，∠C=36°，AD=BD=BC，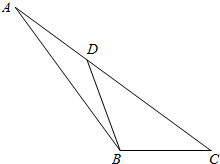
⑤原三角形是钝角三角形，最大角是132°的情况：
如图∠C=132°，∠ABC=36°，AD=BD，CD=CB，
故答案为：72°或90°或108°或126°或132°
点评 本题主要考查了等腰三角形的性质及三角形内角和定理；分情况讨论是解决本题的关键，本题有一定的难度，大部分学生思考没那么全面．
练习册系列答案
相关题目
已知常数a（a是整数）满足下面两个要求：
10．
AD是△ABC的角的平分线，AB=5，AC=3，则S△ABD：S△ABD=（ ）
AD是△ABC的角的平分线，AB=5，AC=3，则S△ABD：S△ABD=（ ）| A． | 1：1 | B． | 2：1 | C． | 5：3 | D． | 3：5 |
20．下列运算正确的是（ ）
| A． | a3•a2=a6 | B． | （a+b）2=a2+b2 | C． | x5+x5=x10 | D． | （-ab）5÷（-ab）2=-a3b3 |
