题目内容
14.在4件同型号的产品中,有1件不合格品和3件合格品.(1)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(2)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,通过大量重复这种试验后发现,抽到合格品的频率稳定在0.9,则可以推算出x的值大约是多少?
分析 (1)用不合格品的数量除以总量即可求得抽到不合格品的概率;
(2)根据频率估计出概率,利用概率公式列式计算即可求得x的值.
解答 解:将不合格记为A,3件合格的记为B1、B2、B3
| A | B1 | B2 | B3 | |
| A | B1A | B2A | B3A | |
| B1 | AB1 | B2B1 | B3B1 | |
| B2 | AB2 | B1B2 | B3B2 | |
| B3 | AB3 | B1B3 | B2B3 |
∴P(B,B)=$\frac{6}{12}$=$\frac{1}{2}$
(2)∵大量重复试验后发现,抽到合格品的频率稳定在0.9,
∴抽到合格品的概率等于0.9,
根据题意得:x+3=0.9(4+x),
解得:x=6.
点评 本题考查了概率的公式、列表法与树状图法及用频率估计概率的知识,解题的关键是了解大量重复试验中事件发生的频率可以估计概率.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
12.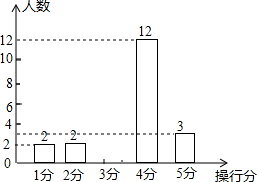 某班有50名同学,男、女生人数各占一半,在本周操行评定中操行得分情况如图统计表中所示,图10是该班本周男生操行得分的条形统计图:
某班有50名同学,男、女生人数各占一半,在本周操行评定中操行得分情况如图统计表中所示,图10是该班本周男生操行得分的条形统计图:
(1)补全统计表和条形统形图;
(2)若要在操行得分为5分的5名同学中选出两名同学作“本周明星”,用画树状图或列表的方法求出选为“本周明星”的正好是一名男同学和一名女同学的概率.
 某班有50名同学,男、女生人数各占一半,在本周操行评定中操行得分情况如图统计表中所示,图10是该班本周男生操行得分的条形统计图:
某班有50名同学,男、女生人数各占一半,在本周操行评定中操行得分情况如图统计表中所示,图10是该班本周男生操行得分的条形统计图:| 操行分得分 | 1分 | 2分 | 3分 | 4分 | 5分 |
| 人数 | 2 | 4 | 9 | 30 | 5 |
(2)若要在操行得分为5分的5名同学中选出两名同学作“本周明星”,用画树状图或列表的方法求出选为“本周明星”的正好是一名男同学和一名女同学的概率.
19.六边形的内角和与外角和的度数分别是( )
| A. | 1080°,180° | B. | 1080°,360° | C. | 720°,180° | D. | 720°,360° |
 已知常数a(a是整数)满足下面两个要求:
已知常数a(a是整数)满足下面两个要求: 已知图1、图2、图3都是4×5的方格纸,其中每个小正方形的边长均为1cm,每个小正方形的顶点称为格点.
已知图1、图2、图3都是4×5的方格纸,其中每个小正方形的边长均为1cm,每个小正方形的顶点称为格点.