题目内容
14.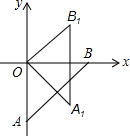 如图,底边长为2的等腰Rt△ABO的边OB在x轴上,将△ABO绕原点O逆时针旋转45°得到△OA1B1,则点A1的坐标为( )
如图,底边长为2的等腰Rt△ABO的边OB在x轴上,将△ABO绕原点O逆时针旋转45°得到△OA1B1,则点A1的坐标为( )| A. | (1,-$\sqrt{2}$) | B. | (1,-1) | C. | ($\sqrt{2},-\sqrt{2}$) | D. | ($\sqrt{2}$,-1) |
分析 A1B1交x轴于H,如图,根据等腰直角三角形的性质得∠OAB=45°,再利用旋转的性质得A1B1=AB=2,∠1=45°,∠OA1B1=45°,则∠2=45°,于是可判断OH⊥A1B1,则根据等腰直角三角形的性质得到OH=A1H=B1H=$\frac{1}{2}$A1B1=1,然后写出点A1的坐标.
解答 解: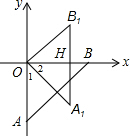 A1B1交x轴于H,如图,
A1B1交x轴于H,如图,
∵△OAB为等腰直角三角形,
∴∠OAB=45°,
∵△ABO绕原点O逆时针旋转45°得到△OA1B1,
∴A1B1=AB=2,∠1=45°,∠OA1B1=45°,
∴∠2=45°,
∴OH⊥A1B1,
∴OH=A1H=B1H=$\frac{1}{2}$A1B1=1,
∴点A1的坐标为(1,-1).
故选B.
点评 本题考查了坐标与图形变换-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.解决本题的关键是判断A1B1被x轴垂直平分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.函数y=$\frac{{a}^{2}+2}{x}$(a为常数)的图象上有三点(-2,y1),(1,y2),(4,y3),则函数值y1、y2、y3的大小关系为( )
| A. | y1<y2<y3 | B. | y2<y3<y${\;}_{{1}_{1}}$ | C. | y1<y3<y2 | D. | y3<y2<y1 |
5.分解因式2x2-2y2结果正确的是( )
| A. | 2(x2-y2) | B. | 2(x+y)(x-y) | C. | 2(x+y)2 | D. | 2(x-y)2 |
9. 如图,AB、CD都是⊙O的弦,且AB⊥CD,若∠CDB=57°,则∠ACD的度数为( )
如图,AB、CD都是⊙O的弦,且AB⊥CD,若∠CDB=57°,则∠ACD的度数为( )
 如图,AB、CD都是⊙O的弦,且AB⊥CD,若∠CDB=57°,则∠ACD的度数为( )
如图,AB、CD都是⊙O的弦,且AB⊥CD,若∠CDB=57°,则∠ACD的度数为( )| A. | 33° | B. | 34° | C. | 43° | D. | 57° |
19.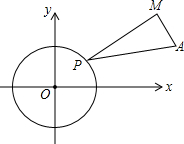 如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )
如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )
 如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )
如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
6.已知a+b=3,ab=2,则a2+b2=( )
| A. | 4 | B. | 6 | C. | 3 | D. | 5 |
4.下列运算正确的是( )
| A. | 3x-x=2 | B. | (3x2)3=9x6 | C. | (a+2)2=a2+4 | D. | $\sqrt{27}$÷$\sqrt{3}$=3 |
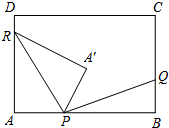 如图,在矩形ABCD中,AB=8k,BC=5k(k为常数,且k>0),动点P在AB边上(点P不与A、B重合),点Q、R分别在BC、DA边上,且AP:BQ:DR=3:2:1.点A关于直线PR的对称点为A′,连接PA′、RA′、PQ.
如图,在矩形ABCD中,AB=8k,BC=5k(k为常数,且k>0),动点P在AB边上(点P不与A、B重合),点Q、R分别在BC、DA边上,且AP:BQ:DR=3:2:1.点A关于直线PR的对称点为A′,连接PA′、RA′、PQ.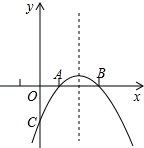 已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).