题目内容
4.函数y=$\frac{{a}^{2}+2}{x}$(a为常数)的图象上有三点(-2,y1),(1,y2),(4,y3),则函数值y1、y2、y3的大小关系为( )| A. | y1<y2<y3 | B. | y2<y3<y${\;}_{{1}_{1}}$ | C. | y1<y3<y2 | D. | y3<y2<y1 |
分析 先根据函数的解析式判断出函数图象所在的象限,再根据各点横坐标的值即可得出结论.
解答 解:∵函数y=$\frac{{a}^{2}+2}{x}$(a为常数)中,k=a2+2>0,
∴函数图象的两个分支分别位于一三象限,且在每一象限内,y随x的增大而减小.
∵-2<0,4>1>0,
∴点(-2,y1)位于第三象限,点(1,y2),(4,y3)位于第一象限,
∴y1<y3<y2.
故选C.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
15.平面直角坐标系内,点A(n,n-1)一定不在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.下列汽车标志中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.按括号内的要求,用四舍五入法,对1022.0099取近似值,其中正确的是有( )个.
①1022.01(精确到0.001)
②0.1022万(精确到个位)
③1020(精确到十位)
④1022.010(精确到千分位)
①1022.01(精确到0.001)
②0.1022万(精确到个位)
③1020(精确到十位)
④1022.010(精确到千分位)
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.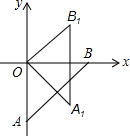 如图,底边长为2的等腰Rt△ABO的边OB在x轴上,将△ABO绕原点O逆时针旋转45°得到△OA1B1,则点A1的坐标为( )
如图,底边长为2的等腰Rt△ABO的边OB在x轴上,将△ABO绕原点O逆时针旋转45°得到△OA1B1,则点A1的坐标为( )
 如图,底边长为2的等腰Rt△ABO的边OB在x轴上,将△ABO绕原点O逆时针旋转45°得到△OA1B1,则点A1的坐标为( )
如图,底边长为2的等腰Rt△ABO的边OB在x轴上,将△ABO绕原点O逆时针旋转45°得到△OA1B1,则点A1的坐标为( )| A. | (1,-$\sqrt{2}$) | B. | (1,-1) | C. | ($\sqrt{2},-\sqrt{2}$) | D. | ($\sqrt{2}$,-1) |
 在娱乐节目“墙来了!”中,参赛选手背靠水池,迎面冲来一堵泡沫墙,墙上有人物造型的空洞.选手需要按墙上的造型摆出相同的姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一块几何体恰好能以右图中两个不同形状的“姿势”分别穿过这两个空洞,则该几何体为( )
在娱乐节目“墙来了!”中,参赛选手背靠水池,迎面冲来一堵泡沫墙,墙上有人物造型的空洞.选手需要按墙上的造型摆出相同的姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一块几何体恰好能以右图中两个不同形状的“姿势”分别穿过这两个空洞,则该几何体为( )


