题目内容
如图所示,直角三角形ABC中,四边形DECF是正方形,观察图(1)和图(2),请回答下列问题:

(1)请简述由图(1)变换成图(2)的形成过程;
(2)证明:∠A1DB=90°;
(3)若AD=3,BD=4,△ADE与△BDF的面积和是 (直接写答案)

(1)请简述由图(1)变换成图(2)的形成过程;
(2)证明:∠A1DB=90°;
(3)若AD=3,BD=4,△ADE与△BDF的面积和是
考点:旋转的性质
专题:
分析:(1)观察图形,发现DA旋转到DA1,DE旋转到DF,而∠EDF=90°,由旋转的定义即可描述由图(1)变成图(2)的形成过程;
(2)根据旋转的性质可得∠ADA1=90°,再根据平角的定义证明;
(3)由图形的旋转可知,图形顺时针旋转了90°,即∠EDF=∠ADA1=90°,可得∠A1DB=90°,△ADE和△BDF面积的和即为△A1DB的面积.
(2)根据旋转的性质可得∠ADA1=90°,再根据平角的定义证明;
(3)由图形的旋转可知,图形顺时针旋转了90°,即∠EDF=∠ADA1=90°,可得∠A1DB=90°,△ADE和△BDF面积的和即为△A1DB的面积.
解答:(1)解:∵四边形DECF为正方形,
∴∠EDF=90°,DE=DF,
∴DA绕点D逆时针旋转90度到DA1的位置,DE绕点D逆时针旋转90度到DF位置,
∴图1中的△ADE绕点D逆时针旋转90°得到图2;
(2)证明:由旋转的性质,旋转角∠EDF=∠ADA1=90°,
∴∠A1DB=180°-∠ADA1=180°-90°=90°;
(3)解:由旋转得:AD=A1D=3,
∵∠A1DB=90°,
∴S△ADE+S△BDF=S△A1BD=
×A1D×BD=
×3×4=6.
故答案为:6.
∴∠EDF=90°,DE=DF,
∴DA绕点D逆时针旋转90度到DA1的位置,DE绕点D逆时针旋转90度到DF位置,
∴图1中的△ADE绕点D逆时针旋转90°得到图2;
(2)证明:由旋转的性质,旋转角∠EDF=∠ADA1=90°,
∴∠A1DB=180°-∠ADA1=180°-90°=90°;
(3)解:由旋转得:AD=A1D=3,
∵∠A1DB=90°,
∴S△ADE+S△BDF=S△A1BD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:6.
点评:本题考查了旋转的性质,(2)熟记旋转的性质并确定出旋转角的度数是解题的关键,(3)通过旋转将两个图形“移”到同一个图形中去,便于计算面积.

练习册系列答案
相关题目
⊙O的直径是15cm,CD经过圆心O,与⊙O交于C、D两点,垂直弦AB于M,且OM:OC=3:5,则AB=( )
| A、24cm | B、12cm |
| C、6cm | D、3cm |
 已知:在正方形ABCD中,E为BC延长线上一点,连结AE分别交DC、DB于F、G.求证:
已知:在正方形ABCD中,E为BC延长线上一点,连结AE分别交DC、DB于F、G.求证:(1)∠DAG=∠DCG;
(2)AG2=GE•GF;
(3)已知GF=
| 3 |
| 3 |
 如图,y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c(a≠0)经过A,B,C(1,0)三点.
如图,y=-x+3交x轴于点A,交y轴于点B,抛物线y=ax2+bx+c(a≠0)经过A,B,C(1,0)三点.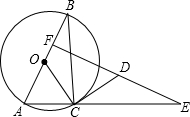 如图,圆O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是圆O的切线,ED⊥AB于F,
如图,圆O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是圆O的切线,ED⊥AB于F, 如图,△ABC中,CD是边AB上的高,且CD2=AD•DB,求证:∠ACB=90°.
如图,△ABC中,CD是边AB上的高,且CD2=AD•DB,求证:∠ACB=90°.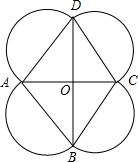 如图是一个花圃培育基地的平面图,此花圃培育基地内部的四边形ABCD是一个平行四边形,花圃周围是分别由边AB,BC,CD,DA为直径的四个半圆,这四个半圆和?ABCD的对角线AC,BD都是通道,已知通道AC与BD相交于点O,经测量得知∠ADC=60°,BC=7cm,OA=3.5m,茗茗从点B出发以顺时针方向沿半圆通道运动,墨墨同时从点D出发以逆时针方向沿半圆通道运动,若茗茗运动的路程s(m)与时间t(s)满足关系:s=
如图是一个花圃培育基地的平面图,此花圃培育基地内部的四边形ABCD是一个平行四边形,花圃周围是分别由边AB,BC,CD,DA为直径的四个半圆,这四个半圆和?ABCD的对角线AC,BD都是通道,已知通道AC与BD相交于点O,经测量得知∠ADC=60°,BC=7cm,OA=3.5m,茗茗从点B出发以顺时针方向沿半圆通道运动,墨墨同时从点D出发以逆时针方向沿半圆通道运动,若茗茗运动的路程s(m)与时间t(s)满足关系:s=