Question

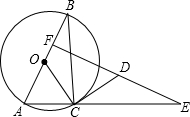如图，圆O是Rt△ABC的外接圆，AB为直径，∠ABC=30°，CD是圆O的切线，ED⊥AB于F，
（1）判断△DCE的形状，并给出合适的说明；
（2）设圆O的半径为2，且OF=

3

-1，求CE、DE的长．

Answer 1

考点：切线的性质,全等三角形的判定与性质,勾股定理

专题：

分析：（1）求出∠A=60°，求出∠OCB=30°，即可求出∠DCE=∠E=30°，根据等腰三角形的判定推出即可；
（2）求出AF，根据AE=2AF即可求出AE，求出CE即可，证△BCO≌△CDE，推出DE=OB即可．

解答：解：（1）△CDE是等腰三角形，
理由是：∵AB是直径，
∴∠ACB=90°，
∵∠ABC=30°，
∴∠BAC=60°，
∵OA=OC，
∴△AOC是等边三角形，
∵CD是切线，
∴∠OCD=90°，
∴∠DCE=180°-90°-60°=30°，
∵ED⊥AB，
∴∠EFA=90°，
∵∠BAC=60°，
∴∠E=30°=∠DCE，
∴DC=DE，即△DCE是等腰三角形；

（2）在Rt△ABC中，∵AB=4，AC=AO=2，
∴BC=

42-22

=2

3

，
∵OF=

3

-1，
∴AE=2AF=2

3

+2，
∴CE=AE-AC=2

3

，
∵∠OCB=∠ACB-∠ACO=30°=∠ABC，
∴在△BCO和△CDE中

∠CBO=∠DCE BC=CE=2 3 ∠BCO=∠E

∴△BCO≌△CDE（ASA），
∴DE=OB=2．

点评：本题考查了勾股定理，切线的性质，等腰三角形的判定，全等三角形的性质和判定的应用，题目综合性比较强，是一道比较好的题目．