Question

5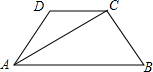．如图，梯形ABCD中，AB∥CD，AD=BC，AC⊥BC，且AC平分∠DAB，∠B=60°，梯形的周长为40cm，则AC=8$\sqrt{3}$cm．

Answer 1

分析 首先根据已知推出四边形ABCD是等腰梯形，再根据周长求出AD=BC=8cm，AB=16cm，再由勾股定理即可求得AC的长．

解答 解：∵AB∥CD，AD=BC，
∴四边形ABCD是等腰梯形，
∴∠DAB=∠B=60°，∠BCD=120°，
∵对角线AC平分∠DAB，AC⊥BC，
∴∠DCA=∠DAC=∠CAB=30°，
∴AD=CD，AB=2BC，
∵梯形周长为40cm，
∴AD=BC=8cm，AB=16cm，
∴AC=$\sqrt{1{6}^{2}-{8}^{2}}$=8$\sqrt{3}$（cm）；
故答案为：8$\sqrt{3}$cm．

点评 本题主要考查梯形了等腰梯形的性质、含30度角的直角三角形的性质、勾股定理；熟练掌握等腰梯形的性质，由30°角的直角三角形的性质求出AB=2BC是解决问题的关键．