题目内容
15. 已知命题“如果两条平行线被第三条直线所截,那么一对同位角的平分线互相平行”
已知命题“如果两条平行线被第三条直线所截,那么一对同位角的平分线互相平行”(1)如图为符合该命题的示意图,请你把该命题用几何符号语言补充完整:已知AB∥CD,EM、FN分别平分∠GEB和∠EFD,则EM∥FD
(2)试判断这个命题的真假,并说明理由.
分析 (1)根据题意写出已知,求证即可;
(2)此命题为真命题,根据平行线的性质得到∠GEB=∠EFD,由角平分线的定义得到∠GEM=$\frac{1}{2}$∠GEB,∠EFN=$\frac{1}{2}$∠EFD,等量代换得到∠GEM=∠EFN,于是得到结论.
解答 解:(1)已知AB∥CD,EM、FN分别平分∠GEB和∠EFD,则EM∥FD;
故答案为:∥,∠GEB,∠EFD,EM∥FD;
(2)此命题为真命题,
证明:∵AB∥CD,
∴∠GEB=∠EFD,
∵EM、FN分别平分∠GEB和∠EFD,
∴∠GEM=$\frac{1}{2}$∠GEB,∠EFN=$\frac{1}{2}$∠EFD,
∴∠GEM=∠EFN,
∴EM∥FD.
点评 此题考查了平行线的判定,解题的关键是:熟记同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
6.下列命题中,假命题的是( )
| A. | 两条直线平行,同位角相等 | B. | 对顶角相等 | ||
| C. | 同位角相等 | D. | 直角都相等 |
10.下列命题中逆命题错误的是( )
| A. | 内错角相等两直线平行 | B. | 直角三角形的两锐角互余 | ||
| C. | 全等三角形的对应边相等 | D. | 互为相反数的两个数的绝对值相等 |
7.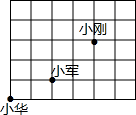 课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )
 课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )| A. | (1,2) | B. | (1,3) | C. | (0,2) | D. | (2,2) |
4.直线l是以二元一次方程8x-4y=5的解为坐标所构成的直线,则该直线不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
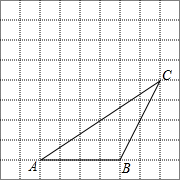 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个长度单位.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个长度单位.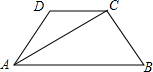 如图,梯形ABCD中,AB∥CD,AD=BC,AC⊥BC,且AC平分∠DAB,∠B=60°,梯形的周长为40cm,则AC=8$\sqrt{3}$cm.
如图,梯形ABCD中,AB∥CD,AD=BC,AC⊥BC,且AC平分∠DAB,∠B=60°,梯形的周长为40cm,则AC=8$\sqrt{3}$cm.