题目内容
10. 如图,D为等边三角形ABC内一点,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,连接DE.
如图,D为等边三角形ABC内一点,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,连接DE.(1)试判定△ADE的形状,并说明理由;
(2)求△DCE的面积.
分析 (1)由旋转的性质得出△ACE≌△ABD得出AE=AD=5.CE=BD=6.∠DAE=60°,得出△ADE是等边三角形,
(2)由△ADE是等边三角形,因此DE=AD=5.作EH⊥CD垂足为H.设DH=x,由勾股定理得出方程,解方程求出DH,由勾股定理求出EH,即可得出△DCE的面积.
解答 解:(1)由旋转的性质得:△ACE≌△ABD,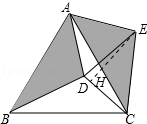
∴AE=AD=5.CE=BD=6.∠DAE=60°.
∴DE=5.
∴AE=AD=DE=5,
∴△ADE是等边三角形,
(2)作EH⊥CD垂足为H.
设DH=x.
由勾股定理得:EH2=CE2-CH2=DE2-DH2,
即62-(4-x)2=52-x2,
解得:x=$\frac{5}{8}$,
∴DH=$\frac{5}{8}$,
由勾股定理得:EH=$\sqrt{D{E}^{2}-D{H}^{2}}=\sqrt{{5}^{2}-(\frac{5}{8})^{2}}=\frac{15}{8}\sqrt{7}$,
∴△DCE的面积=$\frac{1}{2}$CD×EH=$\frac{15\sqrt{7}}{4}$.
点评 本题考查了旋转的性质、勾股定理、等边三角形的判定与性质;熟练掌握旋转的性质,由勾股定理求出DH,EH是解决问题的关键.

练习册系列答案
相关题目
2.下列命题中,为真命题的是( )
| A. | 六边形的内角和为360度 | B. | 多边形的外角和与边数有关 | ||
| C. | 面积相等的三角形全等 | D. | 三角形两边的和大于第三边 |
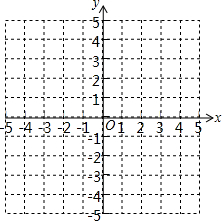 △ABC的三个顶点坐标分别为A(2,-1),B(4,-2),C(1,-3),将△ABC平移至△A1B1C1的位置,点A、B、C对应的点分别为A1、B1、C1,已知点A1的坐标是(-2,3).
△ABC的三个顶点坐标分别为A(2,-1),B(4,-2),C(1,-3),将△ABC平移至△A1B1C1的位置,点A、B、C对应的点分别为A1、B1、C1,已知点A1的坐标是(-2,3).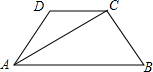 如图,梯形ABCD中,AB∥CD,AD=BC,AC⊥BC,且AC平分∠DAB,∠B=60°,梯形的周长为40cm,则AC=8$\sqrt{3}$cm.
如图,梯形ABCD中,AB∥CD,AD=BC,AC⊥BC,且AC平分∠DAB,∠B=60°,梯形的周长为40cm,则AC=8$\sqrt{3}$cm. 如图,EF∥AD,∠1=∠2,试说明AB∥DG.
如图,EF∥AD,∠1=∠2,试说明AB∥DG. 如图,将直角△ABC沿BC方向平移得到直角△DEF,其中AB=8,BE=10,DM=4,则阴影部分的面积是60.
如图,将直角△ABC沿BC方向平移得到直角△DEF,其中AB=8,BE=10,DM=4,则阴影部分的面积是60.