题目内容
11.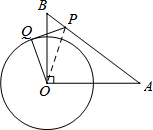 如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x,PQ2=y,则y与x的函数图象大致是( )
如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x,PQ2=y,则y与x的函数图象大致是( )| A. |  | B. |  | C. |  | D. | 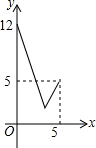 |
分析 根据题意列出函数表达式,即可判断.
解答 解:如图,作PC⊥OA,垂足为C,
∵PC∥BO,
∴△ABO∽△APC,
∴$\frac{AP}{AB}=\frac{PC}{OB}=\frac{AC}{OA}$,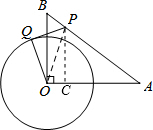
∵AP=x,OA=4,OB=3,
∴PC=$\frac{3}{5}x$,AC=$\frac{4}{5}x$,
∴OC=4-$\frac{4}{5}x$,
∴OP2=(4-$\frac{4}{5}x$)2+($\frac{3}{5}x$)2=x2-$\frac{32}{5}$x+16,
∴y=OP2-OQ2=x2-$\frac{32}{5}$x+12,
当x=0时,y=12,当x=5时,y=5.
故选:A.
点评 本题主要考查了函数的图象与列函数表达式,分析题意弄清题目中的函数关系是做出正确判断的根本.

练习册系列答案
相关题目
10.若一个三角形的两边长分别为5cm,7cm,则第三边长可能是( )
| A. | 2cm | B. | 10cm | C. | 12cm | D. | 14cm |
16.在平面直角坐标系中,点($\sqrt{3}$,1)绕原点顺时针旋转60°后得到点( )
| A. | ($\sqrt{3}$,-1) | B. | (-1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,1) | D. | (1,-$\sqrt{3}$) |
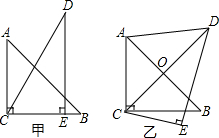
3. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
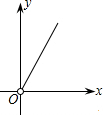
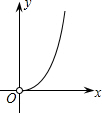
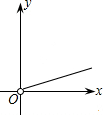
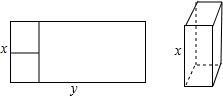 如图,在矩形中截取两个相同的正方形作为立方体的上下底面,剩余的矩形作为立方体的侧面,刚好能组成立方体.设矩形的长和宽分别为y和x,则y与x的函数图象大致是( )
如图,在矩形中截取两个相同的正方形作为立方体的上下底面,剩余的矩形作为立方体的侧面,刚好能组成立方体.设矩形的长和宽分别为y和x,则y与x的函数图象大致是( )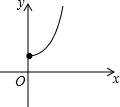
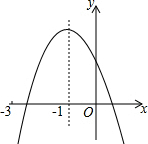 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )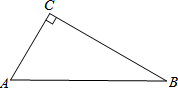 在Rt△ABC中,∠ACB=90°.
在Rt△ABC中,∠ACB=90°.