题目内容
16.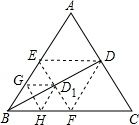 如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2,依次折叠,则BDn=$\frac{\sqrt{3}}{{2}^{n+1}}$.
如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2,依次折叠,则BDn=$\frac{\sqrt{3}}{{2}^{n+1}}$.
分析 根据等边三角形的性质依次求出边上的高,找出规律即可得到结果.
解答 解:∵△ABC是边长为1的等边三角形,BD为AC边上的高,
∴BD=$\frac{\sqrt{3}}{2}$,
∵△BEF是边长为$\frac{1}{2}$等边三角形,
∴BD1=$\frac{\sqrt{3}}{{2}^{2}}$,
∴BD2=$\frac{\sqrt{3}}{{2}^{3}}$,
…
∴BDn=$\frac{\sqrt{3}}{{2}^{n+1}}$,
故答案为:$\frac{\sqrt{3}}{{2}^{n+1}}$.
点评 本题考查了翻折变换-折叠问题,等边三角形的性质,根据已知条件找出规律是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
7.下列命题是假命题的是( )
| A. | 垂线段最短 | |
| B. | 对顶角相等 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条 |
4.-2-1的结果是( )
| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
1.下列运算正确的是( )
| A. | x3•x2=x5 | B. | (x3)2=x5 | C. | (x+1)2=x2+1 | D. | (2x)2=2x2 |
16.在平面直角坐标系中,点($\sqrt{3}$,1)绕原点顺时针旋转60°后得到点( )
| A. | ($\sqrt{3}$,-1) | B. | (-1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,1) | D. | (1,-$\sqrt{3}$) |
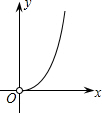
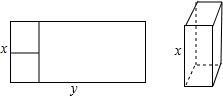 如图,在矩形中截取两个相同的正方形作为立方体的上下底面,剩余的矩形作为立方体的侧面,刚好能组成立方体.设矩形的长和宽分别为y和x,则y与x的函数图象大致是( )
如图,在矩形中截取两个相同的正方形作为立方体的上下底面,剩余的矩形作为立方体的侧面,刚好能组成立方体.设矩形的长和宽分别为y和x,则y与x的函数图象大致是( )
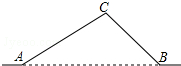 如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.
如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.