题目内容
10.函教y=-x2-4x+1,当a≤x≤b(b>a>-2)时的最大值是4,最小值时-4,求a,b的值.分析 根据抛物线对称轴的位置得出x=a时,y取得最大值4,x=b时y取得最小值-4,然后列出方程即可解决问题.
解答 解:抛物线y=-x2-4x+1的对称轴x=-2,a=-1,开口向下,
∵a≤x≤b(b>a>-2)时的最大值是4,最小值时-4,
∴x=a时,y取得最大值4,x=b时y取得最小值-4.
y=4时,-x2-4x+1=4,解得x=-3或-1,
y=-4时,-x2-4x+1=-4解得x=-5或1,
∴a=-1,b=1.
点评 本题考查二次函数的性质、解题的关键是灵活运用函数的性质解决问题,能根据函数图象确定x=a时,y取得最大值4,x=b时y取得最小值-4,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列计算正确的是( )
| A. | 2a2-4a2=-2 | B. | 3a+a=3a2 | C. | 5b•b=5b2 | D. | 4a6÷2a3=2a2 |
20.下列运算正确的是( )
| A. | (2x-3)2=4x2+12x-9 | B. | (-3a-2)2=9a2+12a+4 | ||
| C. | (a+b)(a+b)=a2+b2 | D. | (2m+3)(2m-3)=4m2-3 |
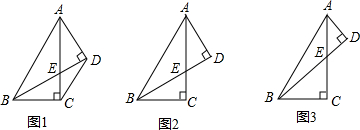
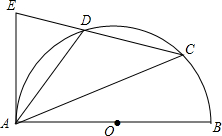 如图,AB是半圆⊙O的直径,点C是半圆上一个动点(不与点A,B重合),点D是弧AC的中点,延长CD交经过点A的切线于点E,连接AD,当△ADE是等腰三角形时,求∠BAC的度数.
如图,AB是半圆⊙O的直径,点C是半圆上一个动点(不与点A,B重合),点D是弧AC的中点,延长CD交经过点A的切线于点E,连接AD,当△ADE是等腰三角形时,求∠BAC的度数.