题目内容
1.已知在以AB为斜边的两个直角△ABD和△ABC中,∠ACB=∠ADB=90°,AC平分∠BAD,AC交BD于E.(1)如图1,若CD∥AB.直接写出$\frac{CD}{AB}$=$\frac{1}{2}$?
(2)当AE=2EC时,求证:△ABC≌△BAD;
(3)试探究AB与AD满足怎样的数量关系时,恰好使E为AC的中点?说明理由.
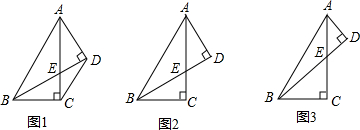
分析 (1)结论:$\frac{CD}{AB}$=$\frac{1}{2}$.如图1中,延长AD、BC交于点M,先证明AB=AM,再证明AD=DM即可.
(2)如图2中,延长AD、BC交于点M,作MN∥AC交BD的延长线于N,根据中位线定理证明AE=MN,再证明△ADE≌△MDN得AD=DM,进一步推出AB=AM=BM,由此即可证明.
(3)结论:AB=3AD.如图3中,延长AD、BC交于点M,作MN∥AC交BD的延长线于N,先证明MN=2AE,再由AE∥MN,得到$\frac{AD}{DM}$=$\frac{AE}{MN}$=$\frac{1}{2}$,由此即可证明.
解答 (1) 解:$\frac{CD}{AB}$=$\frac{1}{2}$.
解:$\frac{CD}{AB}$=$\frac{1}{2}$.
理由:如图1中,延长AD、BC交于点M.
∵CA平分∠BAM,
∴∠CAB=∠CAM,
∵∠CAB+∠ABC=90°,∠CAM+∠M=90°,
∴∠CBA=∠M,
∴AB=AM,
∵AC⊥BM,
∴BC=BM,
∵CD∥AB,
∴AD=DM=$\frac{1}{2}$AM=$\frac{1}{2}$AB,
∴$\frac{AD}{AB}$=$\frac{1}{2}$,
故答案为$\frac{1}{2}$,
(2)如图2中,延长AD、BC交于点M,作MN∥AC交BD的延长线于N.
由(1)可知BC=CM,∵EC∥MN,
∴BE=EN,MN=2EC,
∵AE=2EC,
∴AE=MN,∠AED=∠N,
在△ADE和△MDN中,
$\left\{\begin{array}{l}{∠ADE=∠MDN}\\{∠AED=∠N}\\{AE=MN}\end{array}\right.$,
∴△ADE≌△MDN,
∴AD=DM,
∵BD⊥AM,
∴BA=BM,∵AB-=AM,
∴AB=BM=AM,
∴∠ABC=∠BAD=60°,
在△ABC和△BAD中,
$\left\{\begin{array}{l}{∠ACB=∠ADB=90°}\\{∠ABC=∠BAD}\\{AB=BA}\end{array}\right.$,
△ABC≌△BAD.
(3)结论:AB=3AD.
理由:如图3中,延长AD、BC交于点M,作MN∥AC交BD的延长线于N.
由(2)可知MN=2EC,
∵AE=EC,
∴MN=2AE,
∵AE∥MN,
∴$\frac{AD}{DM}$=$\frac{AE}{MN}$=$\frac{1}{2}$,
∴DM=2AD,AM=3AD,
∵AB=AM,
∴AB=3AD.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是添加辅助线构造全等三角形,学会辅助线的添加方法,属于中考常考题型.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | 2.5×10-7米 | B. | 2.5×10-6米 | C. | 2.5×107米 | D. | 2.5×106米 |
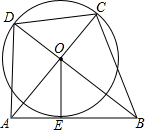 如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BD的延长线交⊙O于C、D.若⊙O的半径为1,则四边形ABCD面积最小值为( )
如图,Rt△AOB中,OA⊥OB,⊙O与AB相切于点E,AO、BD的延长线交⊙O于C、D.若⊙O的半径为1,则四边形ABCD面积最小值为( )| A. | 2+3$\sqrt{2}$ | B. | $\frac{3+2\sqrt{2}}{2}$ | C. | 4+2$\sqrt{2}$ | D. | 3+3$\sqrt{2}$ |
| A. | (a+b)2=a2+b2 | B. | 2a3•3a2=6a6 | C. | (-2x3)4=8x12 | D. | (m-n)6÷(n-m)3=(n-m)3 |
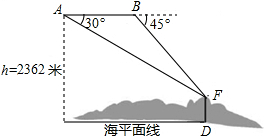 国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图,在一次巡航过程中,巡航飞机飞行高度为2362米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1464米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414)
国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图,在一次巡航过程中,巡航飞机飞行高度为2362米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1464米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414)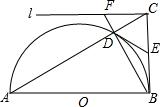 如图,△ABC中,∠ABC=90°,以AB为直径作半圆O,交斜边AC于点D,过点D作半圆O的切线DE,交BC于点E.
如图,△ABC中,∠ABC=90°,以AB为直径作半圆O,交斜边AC于点D,过点D作半圆O的切线DE,交BC于点E.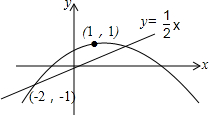 如图,二次函数y=ax2+bx+c的图象经过(-2,-1),(1,1)两点,下列判断:
如图,二次函数y=ax2+bx+c的图象经过(-2,-1),(1,1)两点,下列判断: