题目内容
15.已知一个三角形的两边长分别是2和7,第三边为偶数,则此三角形的周长是( )| A. | 15 | B. | 16 | C. | 17 | D. | 15或17 |
分析 从边的方面考查三角形形成的条件,利用三角形三边关系定理,先确定第三边的范围,进而就可以求出第三边的长,从而求得三角形的周长.
解答 解:设第三边为acm,根据三角形的三边关系可得:7-2<a<7+2.
即:5<a<9,
由于第三边的长为偶数,
则a可以为6cm或8cm.
∴三角形的周长是 2+7+6=15或2+7+8=17.
故选D.
点评 此题主要考查了三角形三边关系,要注意三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列命题错误的是( )
| A. | 矩形的对角线相等 | |
| B. | 平行四边形的对角线互相平分 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相垂直平分的四边形是菱形 |
7.某玩具店试销售一种进价为20元的新型玩具,根据物价部门规定:该玩具售价不得超过90元.在连续七天的试销售过程中,玩具店就销售量y(个)与售价x(元)之间的变化关系做了如表记录.
(1)运用所学过的函数知识,试判断y与x之间的函数关系,并求y与x的函数关系式;
(2)该玩具店若想每天获得2400元的利润,应将售价定为多少元?
(3)这种新型玩具的售价定为多少元时,玩具店每天能够获得的利润w(元)最大?此时的最大利润为多少元?
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 售价x | 30 | 30 | 35 | 40 | 40 | 40 | 45 |
| 销售量y | 100 | 100 | 95 | 90 | 90 | 90 | 85 |
(2)该玩具店若想每天获得2400元的利润,应将售价定为多少元?
(3)这种新型玩具的售价定为多少元时,玩具店每天能够获得的利润w(元)最大?此时的最大利润为多少元?
 如图,△ABC在方格中位置如图所示,A(1,4),B(-2,2).
如图,△ABC在方格中位置如图所示,A(1,4),B(-2,2).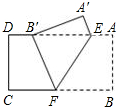 如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上,的点B′处,点A落在点A′处,若AE=6,BF=10,则AB=8.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上,的点B′处,点A落在点A′处,若AE=6,BF=10,则AB=8.