题目内容
2.在△ABC中,AC=2$\sqrt{5}$,点D为直线AB上一点,且AB=3BD,直线CD与直线BC所成锐角的正切值为$\frac{1}{2}$,并且CD⊥AC,则BC的长为$\frac{5}{2}$或5.分析 如图1中,当点D在AB的延长线上时,作BE⊥CD垂足为E,先求出BE,EC,在RT△BCE中利用勾股定理即可解决,如图2中,当点D在线段AB上时,作BE⊥CD于E,方法类似第一种情形.
解答 解:如图1中,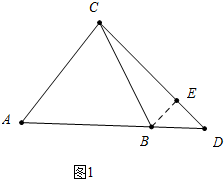 当点D在AB的延长线上时,作BE⊥CD垂足为E,
当点D在AB的延长线上时,作BE⊥CD垂足为E,
∵AC⊥CD,
∴AC∥BE,
∴$\frac{BE}{AC}$=$\frac{DB}{DA}$=$\frac{1}{4}$,
∵$AC=2\sqrt{5}$,
∴BE=$\frac{1}{2}$$\sqrt{5}$,
∵tan$∠BCE=\frac{1}{2}$,
∴EC=2BE=$\sqrt{5}$,
∴BC=$\sqrt{C{E}^{2}+B{E}^{2}}$=$\sqrt{(\frac{1}{2}\sqrt{5})^{2}+(\sqrt{5})^{2}}$=$\frac{5}{2}$.
如图2中,当点D在线段AB上时,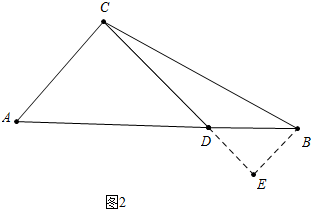
作BE⊥CD于E,
∵AC∥BE,AC=2$\sqrt{5}$,
∴$\frac{BE}{AC}$=$\frac{BD}{AD}$=$\frac{1}{2}$,
∴BE=$\sqrt{5}$,
∵tan∠BCE=$\frac{1}{2}$,
∴EC=2BE=2$\sqrt{5}$,
∴BC=$\sqrt{C{E}^{2}+B{E}^{2}}$=5.
故答案为$\frac{5}{2}$或5.
点评 本题考查平行线的性质、锐角三角函数、勾股定理等知识,解题的关键是添加辅助线,利用平行线的性质解决问题,属于中考常考题型.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
15.已知一个三角形的两边长分别是2和7,第三边为偶数,则此三角形的周长是( )
| A. | 15 | B. | 16 | C. | 17 | D. | 15或17 |
13.2016年2月3日,广州恒大淘宝足球俱乐部官方宣布与西甲传统劲旅马德里竞技队神锋、哥伦比亚现役国脚马丁内斯正式签约,转会费为4200万欧元(约合人民币3.1亿元),签约四年,其中人民币3.1亿元用科学记数法可以表示为( )元.
| A. | 3.1×107 | B. | 3.1×108 | C. | 31×107 | D. | 0.31×109 |
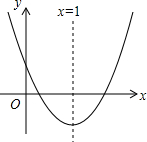 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与y轴的正半轴相交,顶点在第四象限,下列结论:①am2+bm=a(2-m)2+b(2-m);②a+b<0;③$\frac{c}{a}$<1,其中正确的结论个数为( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与y轴的正半轴相交,顶点在第四象限,下列结论:①am2+bm=a(2-m)2+b(2-m);②a+b<0;③$\frac{c}{a}$<1,其中正确的结论个数为( )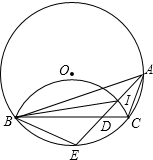 如图,已知△ABC内接于⊙O,点E在弧BC上,AE交BC于点D,EB2=ED•EA经过B、C两点的圆弧交AE于I.
如图,已知△ABC内接于⊙O,点E在弧BC上,AE交BC于点D,EB2=ED•EA经过B、C两点的圆弧交AE于I.