题目内容
1.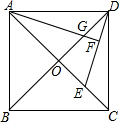 如图,正方形ABCD的两条对角线相交于点O.点E是OC的中点,连接DE,过点A作AF⊥DE于点F,交OD于点G.若正方形的边长为4$\sqrt{2}$,则DF=$\frac{4\sqrt{5}}{5}$.
如图,正方形ABCD的两条对角线相交于点O.点E是OC的中点,连接DE,过点A作AF⊥DE于点F,交OD于点G.若正方形的边长为4$\sqrt{2}$,则DF=$\frac{4\sqrt{5}}{5}$.
分析 根据S△ADE=$\frac{1}{2}$•AE•DO=$\frac{1}{2}$•DE•AF,可得AF=$\frac{12\sqrt{5}}{5}$,在Rt△ADF中,DF=$\sqrt{A{D}^{2}-A{F}^{2}}$,由此即可解决问题.
解答 解: ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4$\sqrt{2}$,AC⊥BD,
∴OA=OC=OD=OB=4,
∵OE=EC=3,
在Rt△DOE中.DE=$\sqrt{O{D}^{2}+O{E}^{2}}$=2$\sqrt{5}$,
∵S△ADE=$\frac{1}{2}$•AE•DO=$\frac{1}{2}$•DE•AF,
∴AF=$\frac{12\sqrt{5}}{5}$,
在Rt△ADF中,DF=$\sqrt{A{D}^{2}-A{F}^{2}}$=$\sqrt{(4\sqrt{2})^{2}-(\frac{12\sqrt{5}}{5})^{2}}$=$\frac{4\sqrt{5}}{5}$.
故答案为$\frac{4\sqrt{5}}{5}$.
点评 本题考查正方形的性质、勾股定理、三角形的面积等知识,解题的关键是学会利用面积法解决一个问题,属于中考常考题型.

练习册系列答案
相关题目
 如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.
如图,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.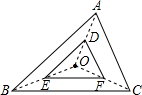 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,$\frac{OD}{DA}$=$\frac{2}{3}$,则△DEF与△ABC的面积比是4:25.
如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,$\frac{OD}{DA}$=$\frac{2}{3}$,则△DEF与△ABC的面积比是4:25. 如图,一个长方形推拉窗,窗高1.5m,则活动窗的通风面积S(m2)与拉开长度b(m)的关系式是S=1.5b.
如图,一个长方形推拉窗,窗高1.5m,则活动窗的通风面积S(m2)与拉开长度b(m)的关系式是S=1.5b. 已知:如图,在?ABCD中,E、F是对角线BD上的两点,BE=DF,求证:AE=CF.
已知:如图,在?ABCD中,E、F是对角线BD上的两点,BE=DF,求证:AE=CF.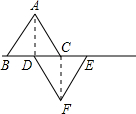 如图,已知△ABC和△DEF是两个边长都为1cm的等边三角形,且B、D、C、E都在同一直线上,连接AD、CF.
如图,已知△ABC和△DEF是两个边长都为1cm的等边三角形,且B、D、C、E都在同一直线上,连接AD、CF. 如图,四边形ABCD是平行四边形,E,F分别为BC,AD的中点,
如图,四边形ABCD是平行四边形,E,F分别为BC,AD的中点,