题目内容
9. 如图,在直角坐标系中,第一次将△OAB变换成△O1A1B1,第二次将△O1A1B1变换成△O2A2B2,第三次将△O2A2B2变换成△O3A3B3.已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0),B1(4,0),B2(8,0),B3(16,0).
如图,在直角坐标系中,第一次将△OAB变换成△O1A1B1,第二次将△O1A1B1变换成△O2A2B2,第三次将△O2A2B2变换成△O3A3B3.已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0),B1(4,0),B2(8,0),B3(16,0).(1)观察每次变换后的三角形有何变化,找出规律,按此规律再将△O3A3B3变换成△O4A4B4,则点A4的坐标是(16,4),B4的坐标是(32,0).
(2)若按第一题找到的规律将△OAB进行了n次变换,得到△OnAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,推测An的坐标是(2n,4),Bn的坐标是(2n+1,0).
分析 (1)根据题目中的信息可以发现A1、A2、A3各点坐标的关系为横坐标是2n,纵坐标都是4,故可求得A4的坐标;B1、B2、B3各点的坐标的关系为横坐标是2n+1,纵坐标都为0,从而可求得点B4的坐标.
(2)根据(1)中发现的规律可以求得An、Bn点的坐标.
解答 解:(1)∵A1(2,4),A2(4,4),A3(8,4),
∴A4的横坐标为:24=16,纵坐标为:4,
∴点A4的坐标为:(16,4).
又∵B1(4,0),B2(8,0),B3(16,0),
∴B4的横坐标为:25=32,纵坐标为:0,
∴点B4的坐标为:(32,0).
故答案为(16,4),(32,0);
(2)由A1(2,4),A2(4,4),A3(8,4),可以发现它们各点坐标的关系为横坐标是2n,纵坐标都是4.
故An的坐标为:(2n,4).
由B1(4,0),B2(8,0),B3(16,0),可以发现它们各点坐标的关系为横坐标是2n+1,纵坐标都是0.
故Bn的坐标为:(2n+1,0).
故答案为(2n,4),(2n+1,0).
点评 本题考查了规律型:点的坐标,关键是通过题目中的信息发现相应的规律,从而解答问题.

练习册系列答案
相关题目
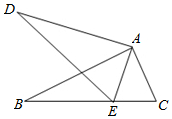 如图,在△ABC和△ADE中,点E在BC边上,∠B=∠D,AB=AD,∠BAD=∠CAE.
如图,在△ABC和△ADE中,点E在BC边上,∠B=∠D,AB=AD,∠BAD=∠CAE.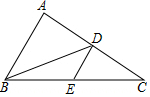 如图,在△ABC中,BD是边AC上的中线,E是BC的中点,连接DE.如果△BDE的面积为2,那么△ABC的面积为8.
如图,在△ABC中,BD是边AC上的中线,E是BC的中点,连接DE.如果△BDE的面积为2,那么△ABC的面积为8.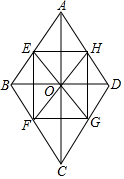 已知菱形ABCD的对角线相交于O,点E、F分别在边AB、BC上,且BE=BF,射线EO、FO分别交边CD、AD于G、H.
已知菱形ABCD的对角线相交于O,点E、F分别在边AB、BC上,且BE=BF,射线EO、FO分别交边CD、AD于G、H.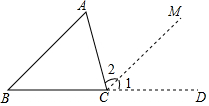 完成下列推理过程
完成下列推理过程 有这样一个问题:探究方程x3-x-2=0的实数根的个数.
有这样一个问题:探究方程x3-x-2=0的实数根的个数. 将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的值.
将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一条边上,求∠1+∠2的值.