题目内容
5.圆锥的底面半径为1,它的侧面展开图的圆心角为180°,则这个圆锥的侧面积为2π.分析 设圆锥的母线长为R,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2π•1=$\frac{180•π•R}{180}$,解得R=2,然后利用扇形的面积公式计算圆锥的侧面积.
解答 解:设圆锥的母线长为R,
根据题意得2π•1=$\frac{180•π•R}{180}$,解得R=2,
所以圆锥的侧面积=$\frac{1}{2}$•2π•1•2=2π.
故答案为2π.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
15. 如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
 如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,有“弘”字一面的相对面上的字是( )| A. | 传 | B. | 统 | C. | 文 | D. | 化 |
16.函数y=$\frac{1}{x-3}$+$\sqrt{x-1}$的自变量x的取值范围是( )
| A. | x≥1 | B. | x≥1且x≠3 | C. | x≠3 | D. | 1≤x≤3 |
20.将一枚质地均匀的硬币先后抛掷两次,则至少出现一次正面向上的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
17.将一次函数y=2x-3的图象沿y轴向上平移8个单位长度,所得直线的解析式为( )
| A. | y=2x-5 | B. | y=2x+5 | C. | y=2x+8 | D. | y=2x-8 |
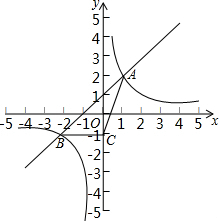 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和-2,这两点的纵坐标之和为1.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+b的图象交于A,B两点,点A和点B的横坐标分别为1和-2,这两点的纵坐标之和为1. 如图,在直角坐标系中,第一次将△OAB变换成△O1A1B1,第二次将△O1A1B1变换成△O2A2B2,第三次将△O2A2B2变换成△O3A3B3.已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0),B1(4,0),B2(8,0),B3(16,0).
如图,在直角坐标系中,第一次将△OAB变换成△O1A1B1,第二次将△O1A1B1变换成△O2A2B2,第三次将△O2A2B2变换成△O3A3B3.已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0),B1(4,0),B2(8,0),B3(16,0).