题目内容
1. 完成下列推理过程
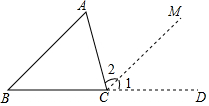
完成下列推理过程已知:△ABC,求证:∠A+∠B+∠C=180°
证明:延长BC到D,作CM∥AB
∴∠A=∠2(两直线平行,内错角相等)
∠B=∠1(两直线平行,同位角相等)
∵∠2+∠1+∠ACB=180° (平角的定义)
∴∠A+∠B+∠ACB=180°(等量代换).
分析 根据平行线的性质得到∠1=∠B,∠2=∠A,而∠1+∠2+∠ACB=180°,利用等量代换可证∠A+∠B+∠ACB=180°.
解答 证明:延长BC到D,作CM∥AB,
∴∠A=∠2(两直线平行,内错角相等),
∠B=∠1(两直线平行,同位角相等),
∵∠2+∠1+∠ACB=180°(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换).
故答案为:∠2;两直线平行,内错角相等;∠1(两直线平行,同位角相等;平角的定义,∠A+∠B+∠ACB=180°;等量代换.
点评 本题考查证明三角形内角和定理,解题的关键是做平行线,利用平行线的性质及平角的定义进行证明.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
17.将一次函数y=2x-3的图象沿y轴向上平移8个单位长度,所得直线的解析式为( )
| A. | y=2x-5 | B. | y=2x+5 | C. | y=2x+8 | D. | y=2x-8 |
 如图,将Rt△ABC沿BC边所在的直线向左平移6个单位,得到Rt△DEF,AB=8,DG=3,则四边形GCFD的面积为39.
如图,将Rt△ABC沿BC边所在的直线向左平移6个单位,得到Rt△DEF,AB=8,DG=3,则四边形GCFD的面积为39. 如图,在直角坐标系中,第一次将△OAB变换成△O1A1B1,第二次将△O1A1B1变换成△O2A2B2,第三次将△O2A2B2变换成△O3A3B3.已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0),B1(4,0),B2(8,0),B3(16,0).
如图,在直角坐标系中,第一次将△OAB变换成△O1A1B1,第二次将△O1A1B1变换成△O2A2B2,第三次将△O2A2B2变换成△O3A3B3.已知A(1,4),A1(2,4),A2(4,4),A3(8,4),B(2,0),B1(4,0),B2(8,0),B3(16,0). 如图,AB⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
如图,AB⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.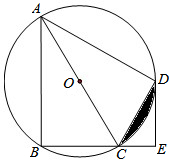 如图,四边形ABCD是⊙O的内接四边形,AC为直径,$\widehat{BD}$=$\widehat{AD}$,DE⊥BC,垂足为E.
如图,四边形ABCD是⊙O的内接四边形,AC为直径,$\widehat{BD}$=$\widehat{AD}$,DE⊥BC,垂足为E.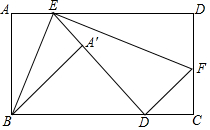 如图,在矩形纸片ABCD中,AB=2,点E在边AD上,沿BE折叠点落在矩形内部的A'处,再把矩形沿EF折叠,使点D落在AC边上的点D'处,旦点E、A'、D'在同一直线上,求AD的最小值.
如图,在矩形纸片ABCD中,AB=2,点E在边AD上,沿BE折叠点落在矩形内部的A'处,再把矩形沿EF折叠,使点D落在AC边上的点D'处,旦点E、A'、D'在同一直线上,求AD的最小值. 如图,将一个等腰直角三角板按如图方式放置在一个矩形纸片上,其中∠α=20°,则∠β的度数为25°.
如图,将一个等腰直角三角板按如图方式放置在一个矩形纸片上,其中∠α=20°,则∠β的度数为25°.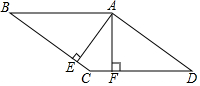 已知如图,?ABCD中,AE⊥BC于E,AF⊥DC于F,AE=3.5,AF=2.8,∠EAF=30°,则AB=7,AD=5.6,BC与AD间的距离是3.5,S?ABCD=19.6.
已知如图,?ABCD中,AE⊥BC于E,AF⊥DC于F,AE=3.5,AF=2.8,∠EAF=30°,则AB=7,AD=5.6,BC与AD间的距离是3.5,S?ABCD=19.6.