题目内容
6.如图1,在等边△ABC中,点D是BC边的中点,点P为AB 边上的一个动点,设AP=x,图1中线段DP的长为y,若表示y与x的函数关系的图象如图2所示,则等边△ABC的面积为( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 12 | D. | 4$\sqrt{3}$ |
分析 从图2的函数图象为抛物线得知,y与x满足二次函数关系,同时y的最小值为$\sqrt{3}$,结合等边三角形的图形可知,当点P运动到DP⊥AD位置时,DP长为最小值,利用等边三角形的特殊角可求出边长,从而得出等边三角形△ABC的面积.
解答 解:由图二可得y最小值=$\sqrt{3}$
∵△ABC为等边三角形,分析图一可知,当P点运动到DP⊥AB时,DP长为最小值
∴此时的DP=$\sqrt{3}$
∵∠B=60°
∴sin60°=$\frac{\sqrt{3}}{BD}$ 解得BD=2
∵D为BC的中点
∴BC=4 连接AD
∵△ABC为等边三角形
∴AD⊥BC
∴tan60°=$\frac{AD}{BD}$
∴AD=2$\sqrt{3}$∴S△ABC=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$
所以选D
点评 本题通过函数图象把动点带来的最小值进行了呈现,正确理解P点运动到何处时DP长最小是关键,同时也考察了学生对函数图象的观察,难度适中.

练习册系列答案
相关题目
17. 如图是一个几何体的三视图,那么这几何体的展开图可以是( )
如图是一个几何体的三视图,那么这几何体的展开图可以是( )
 如图是一个几何体的三视图,那么这几何体的展开图可以是( )
如图是一个几何体的三视图,那么这几何体的展开图可以是( )| A. |  | B. |  | C. |  | D. |  |
11.函数y=$\sqrt{x-3}$中,自变量x的取值范围是( )
| A. | x≠3 | B. | x>3 | C. | x≥3 | D. | x<3 |
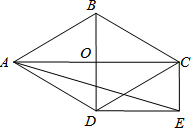 如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.

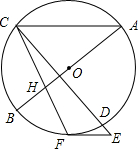 如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E=50°.
如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E=50°.