题目内容
14.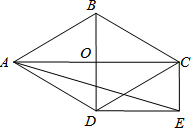 如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2$\sqrt{3}$时,求sin∠AED的值.
分析 (1)根据平行四边形的判定得出边形OCED是平行四边形,根据菱形的性质求出∠COD=90°,根据矩形的判定得出即可;
(2)解直角三角形求出AO、DO、求出AC、CE,根据勾股定理求出AE,解直角三角形求出即可.
解答 (1)证明:∵DE∥AC,CE∥BD,
∴DE∥OC,CE∥OD,
∴四边形OCED是平行四边形,
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COD=90°,
∴四边形OCED是矩形;
(2)解:∵∠ADB=60°,AD=2$\sqrt{3}$,
∴OD=$\sqrt{3}$,AO=3,
∴CE=$\sqrt{3}$,AC=6,
由勾股定理得:AE=$\sqrt{A{C}^{2}+C{E}^{2}}$=$\sqrt{{6}^{2}+(\sqrt{3})^{2}}$=$\sqrt{39}$,
∴sin∠AED=sin∠CAE=$\frac{CE}{AE}$$\frac{\sqrt{3}}{\sqrt{39}}$=$\frac{\sqrt{13}}{13}$.
点评 本题考查了菱形的性质,矩形的判定,平行四边形的判定和性质,勾股定理的应用,能综合运用知识点进行推理是解此题的关键,注意:菱形的对角线互相平分且垂直.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
9.表中给出了变量x与ax2、ax2+bx+c之间的部分对应关系(表格中的符号“--”表示该项数据已经丢失):
(1)求函数y=ax2+bx+c的表达式;
(2)将函数y=ax2+bx+c的图象向左平移1个单位长度,再向上平移2个单位长度,直接写出平移后图象的表达式.
| x | -1 | 0 | 1 |
| ax2 | -- | -- | 1 |
| ax2+bx+c | 7 | 2 | -- |
(2)将函数y=ax2+bx+c的图象向左平移1个单位长度,再向上平移2个单位长度,直接写出平移后图象的表达式.
19.已知⊙O的直径为5,圆心O到直线AB的距离为5,则直线AB与⊙O的位置关系( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 相交或相切 |
6.如图1,在等边△ABC中,点D是BC边的中点,点P为AB 边上的一个动点,设AP=x,图1中线段DP的长为y,若表示y与x的函数关系的图象如图2所示,则等边△ABC的面积为( )


| A. | 4 | B. | 2$\sqrt{3}$ | C. | 12 | D. | 4$\sqrt{3}$ |
 大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷分别标有数字1至6的两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.
大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷分别标有数字1至6的两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品. 如图,四边形ABCD中,∠1=∠2,请你补充一个条件AD=BC,使△ABC≌△CDA.
如图,四边形ABCD中,∠1=∠2,请你补充一个条件AD=BC,使△ABC≌△CDA.