题目内容
1.若点P(x0,y0)在函数y=$\frac{k}{x}$(x<0)的图象上,且x0y0=-1.则它的图象大致是( )| A. |  | B. |  | C. | 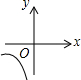 | D. | 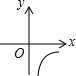 |
分析 根据反比例函数图象是点的坐标特征求得k=-1,即可判定B符合题意.
解答 解:∵点P(x0,y0)在函数y=$\frac{k}{x}$(x<0)的图象上,
∴k=x0y0,
∵x0y0=-1.
∴函数为y=-$\frac{1}{x}$(x<0),
故选B.
点评 本题考查了反比例函数图象是点的坐标特征以及反比例函数的图象,求得系数k的值是解题的关键.

练习册系列答案
相关题目
11.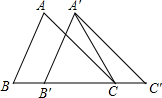 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的面积是( )
如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的面积是( )
 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的面积是( )
如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的面积是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
9.表中给出了变量x与ax2、ax2+bx+c之间的部分对应关系(表格中的符号“--”表示该项数据已经丢失):
(1)求函数y=ax2+bx+c的表达式;
(2)将函数y=ax2+bx+c的图象向左平移1个单位长度,再向上平移2个单位长度,直接写出平移后图象的表达式.
| x | -1 | 0 | 1 |
| ax2 | -- | -- | 1 |
| ax2+bx+c | 7 | 2 | -- |
(2)将函数y=ax2+bx+c的图象向左平移1个单位长度,再向上平移2个单位长度,直接写出平移后图象的表达式.
16.某班5名同学在一周内参加家务劳动的时间如表所示,则关于“劳动时间”的这组数据的中位数是4.
| 劳动时间(小时) | 2 | 3 | 4 | 5 |
| 人数 | 1 | 1 | 2 | 1 |
6.如图1,在等边△ABC中,点D是BC边的中点,点P为AB 边上的一个动点,设AP=x,图1中线段DP的长为y,若表示y与x的函数关系的图象如图2所示,则等边△ABC的面积为( )


| A. | 4 | B. | 2$\sqrt{3}$ | C. | 12 | D. | 4$\sqrt{3}$ |
13. 如图是一个正方体的展开图,把展开图折叠成正方体后,“你”字一面相对的面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,“你”字一面相对的面上的字是( )
 如图是一个正方体的展开图,把展开图折叠成正方体后,“你”字一面相对的面上的字是( )
如图是一个正方体的展开图,把展开图折叠成正方体后,“你”字一面相对的面上的字是( )| A. | 梦 | B. | 我 | C. | 中 | D. | 国 |
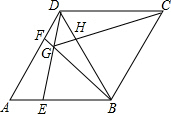 如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: