题目内容
6.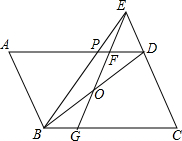 如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.
如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.(1)求证:DF=BG;
(2)若AB=6,AD=9,求DF的长.
分析 (1)连接FB、DG,根据对角线互相平分的四边形是平行四边形得到四边形FBGD是平行四边形,根据平行四边形的性质证明即可;
(2)根据角平分线的定义和相似三角形的判定定理和性质定理计算即可.
解答 (1)证明:连接FB、DG,
∵四边形ABCD是平行四边形,
∴AD∥CD,又BO=OD,
∴GO=OF,
∴四边形FBGD是平行四边形,
∴DF=BG;
(2)∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵AD∥BC,
∴∠APB=∠EBC,
∴∠ABE=∠APB,
∴AP=AB=6,
∴PD=9-6=3,
∵AD∥BC,PD=3,BC=9,
∴$\frac{EP}{EB}$=$\frac{1}{3}$,又BG=DF,
∴PF=$\frac{1}{3}$DF,又PD=3,
∴DF=$\frac{9}{4}$.
点评 本题考查的是平行四边形的性质和相似三角形的判定和性质,掌握相似三角形的对应边的比相等、平行四边形的对边平行且相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.用放大镜将图形放大,应属于哪一种变换( )
| A. | 对称变换 | B. | 平移变换 | C. | 旋转变换 | D. | 相似变换 |
18.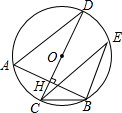 如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )
如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )
 如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )
如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | 3$\sqrt{3}$ |
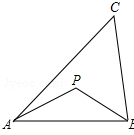 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.举例:如图,若PA=PB,则点P为△ABC的准外心.
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.举例:如图,若PA=PB,则点P为△ABC的准外心.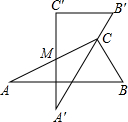 如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于2.5.
如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于2.5.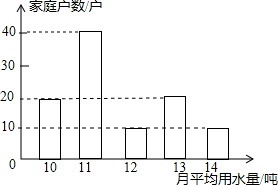 为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.