题目内容
14.直线y=-$\frac{1}{2}$x+3与x轴的交点为(6,0),y随x的增大而减小.分析 分别根据x、y轴上点的坐标特点及一次函数图象的性质进行解答即可.
解答 解:令y=0,则-$\frac{1}{2}$x+3=0,解得x=6,故直线与x轴的交点坐标为:(6,0);
∵直线y=2x-3中k=-$\frac{1}{2}$<0,
∴y随x的增大而减小.
故答案为:(6,0),减小.
点评 本题考查了一次函数图象上点的坐标特征以及一次函数的性质,即一次函数y=kx+b(k≠0)中,当k<0,y随x的增大而减小.

练习册系列答案
相关题目
5.估计$\sqrt{10}$的值在哪两个整数之间( )
| A. | 9和10 | B. | 7和8 | C. | 5和6 | D. | 3和4 |
19.多项式25(m2+n2)2-16(m2-n2)2因式分解的结果是( )
| A. | (9m2+n2)(9n2+m2) | B. | (3m2+n2)(m+3n)(m-3n) | ||
| C. | (9m2+n)(3m-m)(3n-m) | D. | (3m+n)(3m-n)(3n+m)(3n-m) |
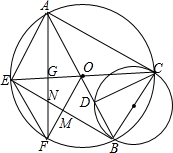 如图,已知四边形AEBC,对角线AB,CE为⊙O的直径,以BC为直径的圆与AB交与点D,连接CD,过点O作OF⊥BE于点M,OF交⊙O于点F,连接AF,交CB于点G,交BE于点N,连接EF.若∠BCD=30°.
如图,已知四边形AEBC,对角线AB,CE为⊙O的直径,以BC为直径的圆与AB交与点D,连接CD,过点O作OF⊥BE于点M,OF交⊙O于点F,连接AF,交CB于点G,交BE于点N,连接EF.若∠BCD=30°.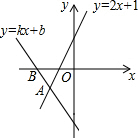 如图,直线y=kx+b与直线y=2x+1相交于点A(-1,-1),则不等式kx+b<2x+1<0的解集为x<-1-1<x<-$\frac{1}{2}$.
如图,直线y=kx+b与直线y=2x+1相交于点A(-1,-1),则不等式kx+b<2x+1<0的解集为x<-1-1<x<-$\frac{1}{2}$.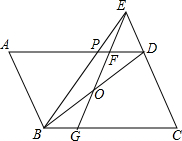 如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.
如图,在?ABCD中,O为对角线BD的中点,BE平分∠ABC且交AD于点P,交CD的延长线于点E;作EO交AD于点F,交BC于点G.