题目内容
平行四边形ABCD中，∠BAD、∠ADC的平分线相交于E，AE、DE与DC、AB延长线交于G、F，求证：AD=DG=GF=FA．考点：平行四边形的性质,全等三角形的判定与性质
专题：证明题
分析：首先根据已知条件和平行四边形的性质可证明△ADE≌△GDE，从而得到AD=DG，AE=FG，同理可得AD=AF，AF=FG，所以AD=DG=GF=FA．
解答：证明：∵四边形ABCD平行四边形，
∴∠BAD+∠ADC=180°，
∵AE、DE分别是∠BAD、∠ADC的平分线，
∴∠DAE+∠ADE=90°，
∴∠AED=∠GED=90°，
在△ADE和△GDE中，
，
∴△ADE≌△GDE（AAS），
∴AD=DG，AE=EG
同理：AD=AF，AF=FG，
∴AD=DG=GF=FA．
∴∠BAD+∠ADC=180°，
∵AE、DE分别是∠BAD、∠ADC的平分线，
∴∠DAE+∠ADE=90°，
∴∠AED=∠GED=90°，
在△ADE和△GDE中，
|
∴△ADE≌△GDE（AAS），
∴AD=DG，AE=EG
同理：AD=AF，AF=FG，
∴AD=DG=GF=FA．
点评：本题考查了平行四边形的性质、全等三角形的判定和性质，题目的综合性较强，是中考常见题型．
练习册系列答案
快捷英语周周练系列答案
相关题目
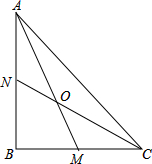如图，在Rt△ABC中，AB=BC=5，BN=BM=3，求△OBC面积．
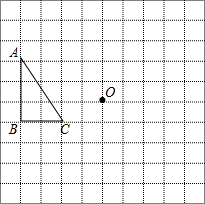在如图的正方形网格中，每个小正方形的边长都是单位1，△ABC的顶点均在格点上．