题目内容
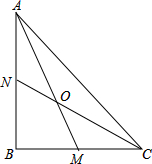如图，在Rt△ABC中，AB=BC=5，BN=BM=3，求△OBC面积．考点：面积及等积变换,相似三角形的判定与性质
专题：
分析：连接MN，可证到△BMN∽△BCA，则有
=
=
，∠BMN=∠BCA，则有MN∥CA，从而得到△OMN∽△OAC，就可求出
、
的值．根据高相等时面积比等于底的比可得
=
=
，从而有S△BOM=
S△BAM．同理可得S△COM=
S△CAM，就可得到S△OBC=S△BOM+S△COM=
S△ABC，然后根据条件就可求出△OBC面积．
| MN |
| CA |
| BN |
| BA |
| 3 |
| 5 |
| OM |
| OA |
| OM |
| AM |
| S△BOM |
| S△BAM |
| OM |
| AM |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
解答：解：连接MN，如图．
∵AB=BC=5，BN=BM=3，
∴
=
=
．
∵∠MBN=∠CBA，
∴△BMN∽△BCA，
∴
=
=
，∠BMN=∠BCA，
∴MN∥CA，
∴△OMN∽△OAC，
∴
=
=
，
∴
=
．
∴
=
=
（等高），
∴S△BOM=
S△BAM．
同理可得：S△COM=
S△CAM．
∴S△OBC=S△BOM+S△COM
=
S△BAM+
S△CAM
=
S△ABC
=
×
×BC×AB
=
×
×5×5
=
．
∴△OBC面积为
．
∵AB=BC=5，BN=BM=3，
∴
| BN |
| BA |
| BM |
| BC |
| 3 |
| 5 |
∵∠MBN=∠CBA，
∴△BMN∽△BCA，
∴
| MN |
| CA |
| BN |
| BA |
| 3 |
| 5 |
∴MN∥CA，
∴△OMN∽△OAC，
∴
| OM |
| OA |
| MN |
| AC |
| 3 |
| 5 |
∴
| OM |
| AM |
| 3 |
| 8 |
∴
| S△BOM |
| S△BAM |
| OM |
| AM |
| 3 |
| 8 |
∴S△BOM=
| 3 |
| 8 |
同理可得：S△COM=
| 3 |
| 8 |
∴S△OBC=S△BOM+S△COM
=
| 3 |
| 8 |
| 3 |
| 8 |
=
| 3 |
| 8 |
=
| 3 |
| 8 |
| 1 |
| 2 |
=
| 3 |
| 8 |
| 1 |
| 2 |
=
| 75 |
| 16 |
∴△OBC面积为
| 75 |
| 16 |
点评：本题考查了相似三角形的判定与性质、高相等时三角形的面积比等于底的比等知识，运用面积法是解决本题的关键，运用面积法可以得到
=
这样一个重要的结论，应该掌握它．
| S△OBC |
| S△ABC |
| OM |
| AM |
练习册系列答案
初中学业考试导与练系列答案
相关题目
平行四边形ABCD中，AC、BD交于O，E为AB上一点，EH∥AC，交BC于H，HO的延长线交AD于F．连接EF．求证：EF∥BD．
平行四边形ABCD中，∠BAD、∠ADC的平分线相交于E，AE、DE与DC、AB延长线交于G、F，求证：AD=DG=GF=FA．
已知O是矩形ABCD的对角线的交点，过点O作OE⊥AC交AB于E，△AOE的面积为5，AE比BC大1，求BD的长．
学校图书馆10月份各类图书的借阅情况如图所示、这个月借阅文学类书籍的人数是数学类的