题目内容
19.计算:(1)$\frac{{a}^{2}}{a+b}$-$\frac{{b}^{2}}{a+b}$;
(2)(-$\frac{b}{2a}$)2•$\frac{6a}{{b}^{2}}$.
分析 (1)根据分式的加法可以解答本题;
(2)根据积的乘方和分式的乘法可以解答本题.
解答 解:(1)$\frac{{a}^{2}}{a+b}$-$\frac{{b}^{2}}{a+b}$
=$\frac{{a}^{2}-{b}^{2}}{a+b}$
=$\frac{(a+b)(a-b)}{a+b}$
=a-b;
(2)(-$\frac{b}{2a}$)2•$\frac{6a}{{b}^{2}}$
=$\frac{{b}^{2}}{4{a}^{2}}•\frac{6a}{{b}^{2}}$
=$\frac{3}{2a}$.
点评 本题考查分式的混合运算,解答本题的关键是明确分式混合运算的计算方法.

练习册系列答案
相关题目
7.若3xm+5y2与x3yn的和是单项式,则mn=( )
| A. | 2 | B. | 4 | C. | 8 | D. | 9 |
14.因式分解x3-2x2+x正确的是( )
| A. | (x-1)2 | B. | x (x-1)2 | C. | x( x2-2x+1) | D. | x (x+1)2 |
11.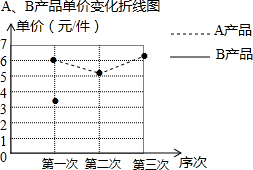 某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
A,B产品单价变化统计表
并求得了A产品三次单价的平均数和方差:
$\overline{{x}_{A}}$=5.9,SA2=$\frac{1}{3}$[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=$\frac{43}{150}$
(1)在折线图中画出B产品的单价变化的情况;
(2)求B产品三次单价的方差;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件的基础上调m%(m>0),但调价后不能超过4元/件,并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
 某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.A,B产品单价变化统计表
| 第一次 | 第二次 | 第三次 | |
| A产品单价(元/件) | 6 | 5.2 | 6.5 |
| B产品单价(元/件) | 3.5 | 4 | 3 |
$\overline{{x}_{A}}$=5.9,SA2=$\frac{1}{3}$[(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]=$\frac{43}{150}$
(1)在折线图中画出B产品的单价变化的情况;
(2)求B产品三次单价的方差;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件的基础上调m%(m>0),但调价后不能超过4元/件,并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
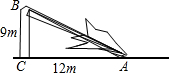 如图,一根树在离地面9米处撕裂,树的顶部落在离底部12米处,求折断之前树高多少米.
如图,一根树在离地面9米处撕裂,树的顶部落在离底部12米处,求折断之前树高多少米. 甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t (h),甲、乙前进的路程与时间的函数图象如图所示.①乙比甲晚出发1小时;②甲比乙晚到B地3小时;③甲的速度是5千米/时;④乙的速度是10千米/小时;根据图象信息,下列说法正确的是( )
甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t (h),甲、乙前进的路程与时间的函数图象如图所示.①乙比甲晚出发1小时;②甲比乙晚到B地3小时;③甲的速度是5千米/时;④乙的速度是10千米/小时;根据图象信息,下列说法正确的是( )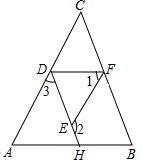 完成推理填空:
完成推理填空: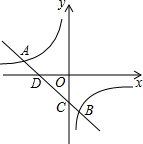 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-3,1),B(2,n)两点,交x轴、y轴于D、C两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-3,1),B(2,n)两点,交x轴、y轴于D、C两点.