题目内容
11.(1)计算:$\sqrt{9}$-(-2)+(-1)0-($\frac{1}{3}$)-1+$\root{3}{27}$(2)比较$\frac{\sqrt{5}-1}{2}$与0.5的大小.
分析 (1)首先计算乘方、开方,然后从左向右依次计算,求出算式的值是多少即可.
(2)应用放缩法,比较$\frac{\sqrt{5}-1}{2}$与0.5的大小即可.
解答 解:(1)$\sqrt{9}$-(-2)+(-1)0-($\frac{1}{3}$)-1+$\root{3}{27}$
=3+2+1-3+3
=6
(2)∵$\frac{\sqrt{5}-1}{2}$>$\frac{2-1}{2}$=$\frac{1}{2}$=0.5,
∴$\frac{\sqrt{5}-1}{2}$>0.5.
点评 此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.

练习册系列答案
相关题目
19.从-3,-2,-1,0,1这五个数中,随机取出一个数,记为a,若a使得关于x的不等式组$\left\{\begin{array}{l}{x-a≤0}\\{x-5<3(x-2)}\end{array}\right.$无解,且关于x的分式方程$\frac{x-1}{x-2}$-$\frac{a}{2-x}$=3有整数解的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
3.单项式-2a的次数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | -2 |
 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.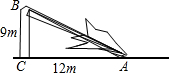 如图,一根树在离地面9米处撕裂,树的顶部落在离底部12米处,求折断之前树高多少米.
如图,一根树在离地面9米处撕裂,树的顶部落在离底部12米处,求折断之前树高多少米.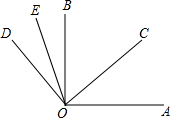 如图,已知∠AOB=90°,∠COE=70°,若OC平分∠AOB,OE平分∠DOB,求:
如图,已知∠AOB=90°,∠COE=70°,若OC平分∠AOB,OE平分∠DOB,求: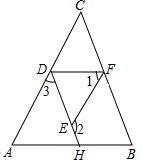 完成推理填空:
完成推理填空: