题目内容
9.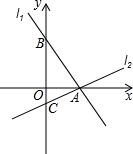 如图,过点A(2,0)的两条直线L1、L2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.
如图,过点A(2,0)的两条直线L1、L2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.(1)求点B的坐标;
(2)若△ABC的面积为4,请求出点C的坐标,并直接写出直线L2所对应的函数关系式.
分析 (1)先根据勾股定理求得BO的长,再写出点B的坐标;
(2)先根据△ABC的面积为4,求得CO的长,再根据点A、C的坐标,运用待定系数法求得直线l2的解析式.
解答 解:(1)∵点A的坐标为(2,0),
∴AO=2,
在直角三角形OAB中,AO2+OB2=AB2,
即22+OB2=($\sqrt{{13}^{2}}$),
∴OB=3,
∴B(0,3);
(2)∵△ABC的面积为4
$\underset{∴}{\;}$4=$\frac{1}{2}$BC×OA,即4=$\frac{1}{2}$BC×2,
∴BC=4,
∴OC=BC-OB=4-3=1,
∴C=(0,1),
设l2的解析式为y=kx+b,则$\left\{\begin{array}{l}{0=2k+b}\\{-1=b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=-1}\end{array}\right.$,
直线L2所对应的函数关系式为y=$\frac{1}{2}$x-1.
点评 本题主要考查了两条直线的交点问题,解题的关键是掌握勾股定理以及待定系数法.注意:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解,反之也成立.

练习册系列答案
相关题目
17. 如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )
如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )
 如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )
如图,AB是半圆O的直径,点C在半圆O上,把半圆沿弦AC折叠,$\widehat{AC}$恰好经过点O,则$\widehat{BC}$与$\widehat{AC}$的关系是( )| A. | $\widehat{BC}$=$\frac{1}{2}$$\widehat{AC}$ | B. | $\widehat{BC}$=$\frac{1}{3}$$\widehat{AC}$ | C. | $\widehat{BC}$=$\widehat{AC}$ | D. | 不能确定 |
14.若关于x的分式方程$\frac{m}{x-3}=\frac{2x}{3-x}+1$有增根,则这个增根是( )
| A. | x=3 | B. | x=1 | C. | x=-1 | D. | x=-3 |
1.已知一个角的补角等于这个角的余角的4倍,则这个角的度数是( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
19.从长度分别为3cm,4cm,6cm,8cm,10cm的五条线段中任取三条,若每条线段被取到的可能性相同,则取到的三条线段可以组成三角形的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{7}{10}$ |
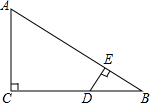 已知:如图,在△ABC中,∠C=90°,D是BC上一点,DE⊥AB于E,若AC=6,AB=10,DE=2.
已知:如图,在△ABC中,∠C=90°,D是BC上一点,DE⊥AB于E,若AC=6,AB=10,DE=2. 完成推理填空:
完成推理填空: 如图,直线AB和CD相交于点O,OE平分∠BOD,∠BOE=30°,那么∠AOD=120度.
如图,直线AB和CD相交于点O,OE平分∠BOD,∠BOE=30°,那么∠AOD=120度.