题目内容
16.下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,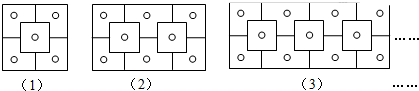
(1)第1个图中所贴剪纸“○”的个数为5,第2个图中所贴剪纸“○”的个数为8,第3个图中所贴剪纸“○”的个数为11;
(2)用代数式表示第n个图中所贴剪纸“○”的个数,并求当n=100时,所贴剪纸“○”的个数.
分析 (1)第一个图中所贴剪纸“○”的个数为3+2=5;第二个图中所贴剪纸“○”的个数为2×3+2=8;第三个图中所贴剪纸“○”的个数为3×3+2=11;…从而可以得出第n个图中所贴剪纸“○”的个数为(3n+2);
(2)利用(1)中的规律代入求得答案即可.
解答 解:(1)第一个图中所贴剪纸“○”的个数为3+2=5;
第二个图中所贴剪纸“○”的个数为2×3+2=8;
第三个图中所贴剪纸“○”的个数为3×3+2=11;
…
第n个图中所贴剪纸“○”的个数为(3n+2);
(2)当n=100时,所贴剪纸“○”的个数为100×3+2=302.
点评 此题考查图形的变化规律.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,得出规律解决问题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
11.观察下图,填表后再回答问题:
(1)在表格中填入正确的数:
(2)试求第6个图形中“●”的个数和“☆”的个数?
(3)试求第n个图形中“●”的个数和“☆”的个数?
| 序号 | 1 | 2 | 3 | … |
| 图形 |  |  |  | … |
| ●的个数 | 8 | 16 | 24 | … |
| ☆的个数 | 1 | 4 | 9 | … |
(2)试求第6个图形中“●”的个数和“☆”的个数?
(3)试求第n个图形中“●”的个数和“☆”的个数?
1.用“O”摆出如图所示的图案,若按照同样的方式构造图案,则第11个图案需要( )个“O”.


| A. | 100 | B. | 145 | C. | 181 | D. | 221 |
5.已知关于x的不等式组$\left\{\begin{array}{l}{x-a>-1}\\{x-a<2}\end{array}\right.$的解集中任意一个x的值均不在0≤x≤4的范围内,则a的取值范围是( )
| A. | a>5或a<-2 | B. | -2≤a≤5 | C. | -2<a<5 | D. | a≥5或a≤-2 |
 如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).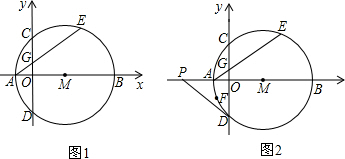
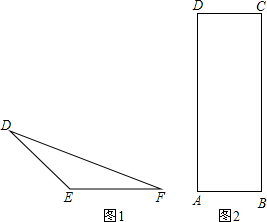 如图,在等腰三角形DEF中,DE=FE=1,∠DEF=135°.
如图,在等腰三角形DEF中,DE=FE=1,∠DEF=135°.