题目内容

11．观察下图，填表后再回答问题：
序号123…
图形
…
●的个数81624…
☆的个数149…
（1）在表格中填入正确的数：
（2）试求第6个图形中“●”的个数和“☆”的个数？
（3）试求第n个图形中“●”的个数和“☆”的个数？

分析 （1）由图中可以看出“●”的个数为4×4=16；“★”的个数为32=9；
（2）（3）易得所有图形中“●”的个数依次为8的1倍，2倍，3倍…；“★”的个数依次为12，22，32…据此可得所求答案．

解答 解：（1）填表如下：

序号123…
图形
…
●的个数81624…
☆的个数149…
（2）∵图形中“●”的个数依次为8的1倍，2倍，3倍…；“★”的个数依次为12，22，32…
∴第6图形中“●”有8×6=48个，“★”有62=36个；
（3）第n图形中“●”有8n个，“★”有n2个；

点评 此题考查图形的变化规律，找出图形之间的联系，得出运算规律，利用规律解决问题．

练习册系列答案
相关题目
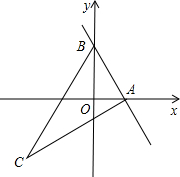6．已知：如图，直线y=kx+2与x轴正半轴相交于A（t，0），与y轴相交于点B，抛物线y=-x2+bx+c经过点A和点B，点C在第三象象限内，且AC⊥AB，tan∠ACB=$\frac{1}{2}$．
（1）当t=1时，求抛物线的表达式；
（2）试用含t的代数式表示点C的坐标；
（3）如果点C在这条抛物线的对称轴上，求t的值．
7．计算：
（1）2$\sqrt{3}$-$\root{3}{8}$-|1-2$\sqrt{3}$|
（2）$\root{3}{0.008}$×$\sqrt{1\frac{9}{16}}$-$\sqrt{81}$+$\root{3}{-\frac{1}{64}}$．
4．计算：（1+2a-3b）2．
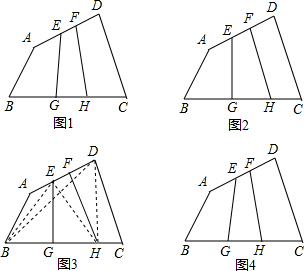6．【提出问题】如图①，在四边形ABCD中，点E、F是AD的n等分点中最中间2个，点G、H是BC的n等分点中最中间2个，（其中n为奇数），连接EG、FH，那么S四边形EFHG与S四边形ABCD之间有什么关系呢？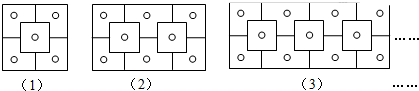
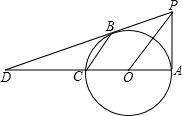【探究发现】：为了解决这个问题，我们可以先从一些简单的、特殊的情形入手：
如图②：四边形ABCD中，点E、F是AD的3等分点，点G、H是BC的3等分点，连接EG、FH，那么S四边形EFHG与S四边形ABCD之间有什么关系呢？
如图③，连接EH、BE、DH，
因为△EGH与△EBH高相等，底的比是1：2，
所以S△EGH=$\frac{1}{2}$S△EBH
因为△EFH与△DEH高相等，底的比是1：2，
所以S△EFH=$\frac{1}{2}$S△DEH
所以S△EGH+S△EFH=$\frac{1}{2}$S△EBH+$\frac{1}{2}$S△DEH
即S四边形EFHG=$\frac{1}{2}$S四边形EBH
连接BD，
因为△DBE与△ABD高相等，底的比是2：3，
所以S△DBE=$\frac{2}{3}$S△ABD
因为△BDH与△BCD高相等，底的比是2：3，
所以S△BDH=$\frac{2}{3}$S△BCD
所以S△DBE+S△BDH=$\frac{2}{3}$S△ABD+$\frac{2}{3}$S△BCD=$\frac{2}{3}$（S△ABD+S△BCD）=$\frac{2}{3}$S四边形ABCD
即S四边形EBHD=$\frac{2}{3}$S四边形ABCD
所以S四边形EFHG=$\frac{1}{2}$S四边形EBHD=$\frac{1}{2}$×$\frac{2}{3}$S四边形ABCD=$\frac{1}{3}$S四边形ABCD
（1）如图④：四边形ABCD中，点E、F是AD的5等分点中最中间2个，点G、H是BC的5等分点中最中间2个，连接EG、FH，猜想：S四边形EFHG与S四边形ABCD之间有什么关系呢S四边形EFHG=$\frac{1}{5}$S四边形ABCD，验证你的猜想：
【问题解决】如图①，在四边形ABCD中，点E、F是AD的n等分点中最中间2个，点G、H是BC的n等分点中最中间2个，连接EG、FH，（其中n为奇数）那么S四边形EFHG与S四边形ABCD之间的关系为：S四边形EFHG=$\frac{1}{n}$S四边形ABCD（不必写出求解过程）
【问题拓展】仿照上面的探究思路，若n为奇数，请再给出一个一般性结论．（画出图形，不必写出求解过程）
16．下列图案是晋商大院窗格的一部分，其中“○”代表窗纸上所贴的剪纸，

（1）第1个图中所贴剪纸“○”的个数为5，第2个图中所贴剪纸“○”的个数为8，第3个图中所贴剪纸“○”的个数为11；
（2）用代数式表示第n个图中所贴剪纸“○”的个数，并求当n=100时，所贴剪纸“○”的个数．
3．如图，两条直线相交只有1个交点，三条直线相交最多有3个交点，四条直线相交最多有6个交点，五条直线相交最多有10个交点，八条直线相交最多有28个交点．
20．以AC=6为直径画一个圆，过点A作AP⊥AC，过点C作CB∥OP，直线PB与直线AC相交于点D．
（1）求证：PD为圆O的切线；
（2）已知PA=$\frac{1}{2}BD$=4，求BC．
1．在直角坐标系中，点O为坐标原点，把抛物线y=-x2先向右平移m个单位，再向上平移n个单位（m＞0，n＞0），得到的新抛物线顶点为P，新抛物线与x轴交于A、B两点（其中点A在点B的左侧），交于y轴负半轴交于C点．
（1）若n=2，△ABC的面积为2$\sqrt{2}$，求m的值．
（2）若点B的横坐标为m+1，点P关于x轴的对称点Q在直线BC上，直线BC的上方的新抛物线上是否存在点M，使△MBC与△PBC的面积相等？若存在，求出点M的坐标；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网