��Ŀ����
11����ͼ�٣���ƽ��ֱ������ϵ�У���ֱ֪��AB��x��y��ֱ���A��-8��0����B��0��6������1������߶�AB�ij���
��2����ͼ�ڣ��ڵ���������һ��C��ʹ��CB��AB����CB=AB�����C�����ꣻ
��3����ͼ�ۣ��ڣ�1����2���������£�����AC����DΪBC���е㣬����D��AC�Ĵ���EF����AC��E����ֱ��AB��F������AD������PΪ����AD�ϵ�һ�����㣬����PC��PF������P������AD���˶�ʱ��PF2-PC2��ֵ�Ƿ����ı䣿���ı䣬������䷶Χ�������䣬������ֵ��
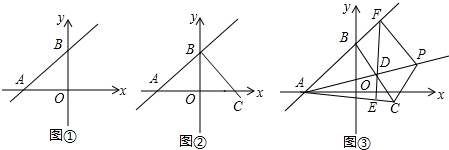
���� ��1����A��B����ȷ����OA��OB�ij������ù��ɶ������AB�ij����ɣ�
��2����ͼ2��ʾ����C��CD��ֱ��y�ᣬ���C���꣬����AAS�õ�������AOB��������BDCȫ�ȣ�����ȫ�������ζ�Ӧ����ȵõ����Ա���ȣ����m��n��ֵ������ȷ����C���ꣻ
��3����ͼ3��ʾ������CF��AP�ڵ�H������SAS�õ�������ABD��������CBFȫ�ȣ�����ȫ�������ζ�Ӧ����ȵõ���BAD=��BCF�����ɶԶ�����ȵõ���CHD=��ABD=90�㣬��CH��ֱ��AP�����ù��ɶ����õ�PF2-PC2=��FH2+PH2��-��CH2+PH2��=PH2-CH2������FH2-CH2=��DF2-DH2��-��DC2-DH2��=DF2-DC2�����BD��DC�ij��������õ�DF�ij���ȷ����PF2-PC2��ֵ���䣬Ϊ25��
���  �⣺��1����A��-8��0����B��0��6����
�⣺��1����A��-8��0����B��0��6����
��OA=8��OB=6��
��AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10��
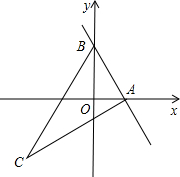
��2����ͼ2��ʾ����C��CD��y�ύ�ڵ�D��
��������C��m��n����m��0��n��0����
��AB=BC����AB��BC��
���BAO+��ABO=��DBC+��ABO=90�㣬
���BAO=��DBC��
�ڡ�AOB�͡�BDC�У�
$\left\{\begin{array}{l}{��AOB=��BDC=90��}\\{��BAO=��CBD}\\{AB=BC}\end{array}\right.$��
���AOB�ա�BDC��AAS����
��BD=OA��DC=OB����6-n=8��m=6��
��n=-2��
��C������6��-2����
��3����ͼ3��ʾ������CF��AP�ڵ�H��
������ã���ABCΪ����ֱ�������Σ�����BAC=��ACB=45�㣬
��EF��AC�����AEFΪ����ֱ�������Σ�
���BFD=45�㣬
���BDFΪ����ֱ�������Σ�
��BF=BD��
�ڡ�ABD�͡�CBF�У�
$\left\{\begin{array}{l}{AB=BC}\\{��ABD=��CBF=90��}\\{BD=BF}\end{array}\right.$��
���ABD�ա�CBF��SAS����
���BAD=��BCF��
�ߡ�ABD=��PDC��
���DHC=��ABC=90�㣬��CF��AP��
��PF2-PC2=��FH2+PH2��-��CH2+PH2��=PH2-CH2��
��FH2-CH2=��DF2-DH2��-��DC2-DH2��=DF2-DC2��
��AB=BC=10��DΪBC���е㣬
��BD=DC=5��
�ߡ�BDFΪ����ֱ�������Σ�
��DF=$\sqrt{2}$BD=5$\sqrt{2}$��
��PF2-PC2=DF2-DC2=25��
��PF2-PC2Ϊ��ֵ25��
���� ��������һ�κ����ۺ��⣬�漰��֪ʶ�У�ȫ�������ε��ж������ʣ����ɶ�����������ͼ�����ʣ�����ֱ�������ε��ж������ʣ���������ȫ�������ε��ж��������ǽⱾ��Ĺؼ���

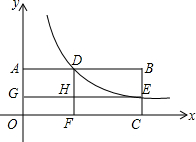 ��ͼ������OABC�Ķ���A��y���ϣ�C��x���ϣ�˫����y=$\frac{k}{x}$��AB���ڵ�D����BC���ڵ�E��DF��x���ڵ�F��EG��y���ڵ�G����DF�ڵ�H��������OGHF�;���HDBE������ֱ���1��2����k��ֵΪ��������
��ͼ������OABC�Ķ���A��y���ϣ�C��x���ϣ�˫����y=$\frac{k}{x}$��AB���ڵ�D����BC���ڵ�E��DF��x���ڵ�F��EG��y���ڵ�G����DF�ڵ�H��������OGHF�;���HDBE������ֱ���1��2����k��ֵΪ��������| A�� | $\frac{12}{5}$ | B�� | $\sqrt{2}$+1 | C�� | $\frac{5}{2}$ | D�� | 2$\sqrt{2}$ |
 ��ͼ���ڷ���ֽ�У�ÿ��С����ı߳�Ϊ1�����߶�AB��BC����ƽ��BC�ij��Ⱥ��߶�AB��ɨ���������10��
��ͼ���ڷ���ֽ�У�ÿ��С����ı߳�Ϊ1�����߶�AB��BC����ƽ��BC�ij��Ⱥ��߶�AB��ɨ���������10�� ��֪����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OMƽ�֡�AOD���ҡ�1����2=1��4��ONƽ�֡�AOC�����BON�Ķ�����
��֪����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OMƽ�֡�AOD���ҡ�1����2=1��4��ONƽ�֡�AOC�����BON�Ķ�����
 ��֪����ͼ��ֱ��y=kx+2��x���������ཻ��A��t��0������y���ཻ�ڵ�B��������y=-x2+bx+c������A�͵�B����C�ڵ����������ڣ���AC��AB��tan��ACB=$\frac{1}{2}$��
��֪����ͼ��ֱ��y=kx+2��x���������ཻ��A��t��0������y���ཻ�ڵ�B��������y=-x2+bx+c������A�͵�B����C�ڵ����������ڣ���AC��AB��tan��ACB=$\frac{1}{2}$��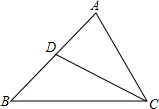 ��ͼ���ڡ�ABC�У�CD��AB���ϵ����ߣ���֪��B=45�㣬tan��ACB=3��AC=$\sqrt{10}$����tan��DCB��ֵ��
��ͼ���ڡ�ABC�У�CD��AB���ϵ����ߣ���֪��B=45�㣬tan��ACB=3��AC=$\sqrt{10}$����tan��DCB��ֵ��